
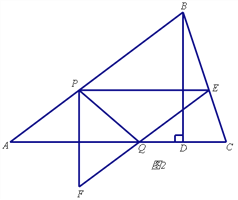
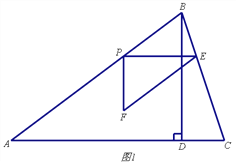
����Ŀ����ͼ1���������ABC�У�AB=5��tanC=3��BD��AC�ڵ�D��BD=3����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���AB���յ�B�˶�������P��PE��AC����BC�ڵ�E����PEΪ����Rt��PEF��ʹ��EPF=90�㣬��F�ڵ�P���·�����EF��AB������PEF����ABD�ص�����ͼ�ε����ΪS��ƽ����λ����S��0������P���˶�ʱ��Ϊt���룩
��t��0����
��1�����߶�AC�ij���
��2������PEF����ABD�ص�����ͼ��Ϊ�ı���ʱ����S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3������EF����ֱ�����AC���ڵ�Q������PQ����ͼ2��ֱ��д����ABC��ijһ���㵽P��Q����������ʱt��ֵ��
���𰸡���1��5��2��S=![]() ��5��t��2��3������������t=
��5��t��2��3������������t=![]() s��
s��![]() s��
s��![]() sʱ��������ĿҪ��
sʱ��������ĿҪ��
������������: ��1����Rt��ABD�У����ù��ɶ������AD����Rt��BDC�У����CD���ɣ�
��2����2��������⣺��ͼ1�У���0��t��1ʱ���ص��������ı���PMDN����ͼ2�У���![]() ��t��5ʱ���ص��������ı���PNMF��
��t��5ʱ���ص��������ı���PNMF��
��3����ͼ5�У���PQ�Ĵ�ֱƽ���߾�����Aʱ������PE=PA���ɵ�t=5-t������⣮��ͼ6�У���PQ�Ĵ�ֱƽ���߾�����Bʱ����EN��AC��N��EP��BD��M����Rt��BQD�У�����BQ2=QD2+BD2���г����̼��ɽ������.
���:
��1����Rt��ABD�У���BDA=90�㣬AB=5��BD=3��
��AD=![]() =
=![]() =4��
=4��
��Rt��BCD�У���BDC=90�㣬BD=3��tanc=3����CD=![]() =
=![]() =1��
=1��
��AC=AD+CD=4+1=5��
��2����ͼ1�У���0��t��1ʱ���ص��������ı���PMDN��
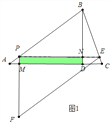


��֪PA=t��AM=![]() t��PM=
t��PM=![]() t��DM=4��
t��DM=4��![]() t��
t��
��S=![]() t��4��
t��4��![]() t��=��
t��=��![]() t2+
t2+![]() t��
t��
��ͼ2�У���![]() ��t��5ʱ���ص��������ı���PNMF��
��t��5ʱ���ص��������ı���PNMF��
��AB=5��AC=AD+CD=4+1=5��
��AC=AB��
��֤PB=PE=5��t��PF=![]() ��5��t����PN=
��5��t����PN=![]() ��5��t����
��5��t����
S=![]() ��5��t��
��5��t��![]() ��5��t����
��5��t����![]()
![]() ��5��t��
��5��t��![]()
![]() ��5��t��=
��5��t��=![]() ��5��t��2��
��5��t��2��
��3����ͼ3�У���A��P��Q�������ʱ��
��֪�ı���APEQʱ���Σ���PE=PA����t=5��t����t=![]() ��
��
��ͼ4�У���B��P��Q�������ʱ����EN��AC��N��EP��BD��M��


��֪�ı���PENG�Ǿ��Σ��ı���DMEN�Ǿ��Σ���PG=EN=![]() t��EM=DN=PE��PM=
t��EM=DN=PE��PM=![]() ��5��t����
��5��t����
QN=![]() EN=
EN=![]() t����QD=4����5��t��=t��1����Rt��BQD����BQ2=QD2+BD2��
t����QD=4����5��t��=t��1����Rt��BQD����BQ2=QD2+BD2��
����5��t��2=32+��t��1��2����t=![]() ��
��
��ͼ5�У���C��P��Q�������ʱ����PM��AC��M������PC��
��PC=CQ���ɵã���![]() t��2+��5��
t��2+��5��![]() t��2=t2�����t=
t��2=t2�����t=![]()
����������t=![]() s��
s��![]() s��
s��![]() sʱ��������ĿҪ��
sʱ��������ĿҪ��
�㾦: ���⿼���������ۺ��⡢��ֱ�������Ρ����ɶ�����������Ǻ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����̽�����⣬�����п�ѹ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ����Ӧ���������£�������ѧ���ı任��ƽ�ơ���ת����Գƣ�֪ʶ�������ɴ�ͼ�α仯��ʹ�õ�A���E�غϡ���B���D�غϣ�д��һ�ֱ仯�Ĺ���_____.
����Ӧ���������£�������ѧ���ı任��ƽ�ơ���ת����Գƣ�֪ʶ�������ɴ�ͼ�α仯��ʹ�õ�A���E�غϡ���B���D�غϣ�д��һ�ֱ仯�Ĺ���_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¶��壺[a��b��c]Ϊ���κ���y=ax2+bx+e��a��0��a��b��cΪʵ��������ͼ���������磺y=-x2+2x+3����ͼ������Ϊ[-1��2��3]
��1�����κ���y=![]() x2-x-1����ͼ������Ϊ ��
x2-x-1����ͼ������Ϊ ��
��2����ͼ��������[m��m+1��m+1]�Ķ��κ�����ͼ����x��ֻ��һ�����㣬��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90����AC=8��BC=6��CD��AB�ڵ�D����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����߶�AB���յ�B�˶������˶������У��Ե�PΪ��������Ϊ2����Ϊ1�ľ���PQMN������PQ=2��PN=1����Q�ڵ�P����࣬MN��PQ���·֣���PQ�ܱ�����AC��ֱ����P���˶�ʱ��Ϊt���룩��t��0��������PQMN����ACD���ص�����ͼ�����ΪS��ƽ����λ����
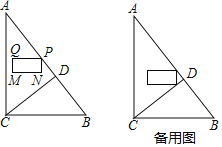
��1�����߶�CD�ij���
��2��������PQMN���߶�CD�й�����ʱ����t��ȡֵ��Χ��
��3������P���߶�AD���˶�ʱ����S��t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2��8ax+12a��a��0����x�ύ��A��B����(��A�ڵ�B�����)��������������һ��C�ڵ�һ���ޣ���ʹ��OCA�ס�OBC��
��1����OC�ij���![]() ��ֵ��
��ֵ��
��2����ֱ��BC��y�ύ��P�㣬����Cǡ����OP�Ĵ�ֱƽ������ʱ����ֱ��BP�������ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳
���ۺ���ʵ�����ϣ���ʦ��ͬѧ����������ƽ����AB��CD��һ�麬60���ǵ�ֱ�����dz�EFG(��EFG��90������EGF��60��)��Ϊ���չ��ѧ���
��������
(1)��ͼ(1)��С�������dzߵ�60���ǵĶ���G����CD�ϣ�����2��2��1�����1�Ķ�����
(2)��ͼ(2)��Сӱ�����dzߵ�������ǵĶ���E��G�ֱ����AB��CD�ϣ�����̽����˵����AEF���FGC֮���������ϵ��
����Ӧ��
(3)��ͼ(3)��С�������dzߵ�ֱ�Ƕ���F����CD�ϣ�30���ǵĶ���E����AB�ϣ�����AEG���������CFG����______(�ú�����ʽ�ӱ�ʾ)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ų�����ֽƬ![]() ����ͼ�٣���
����ͼ�٣���![]() ����ֽƬ�۵���ʹ
����ֽƬ�۵���ʹ![]() ����
����![]() ���ϣ�
���ϣ�![]() Ϊ
Ϊ![]() �Ķ�Ӧ�㣬�ۺ�Ϊ
�Ķ�Ӧ�㣬�ۺ�Ϊ![]() ����ͼ�ڣ����ٽ�������
����ͼ�ڣ����ٽ�������![]() ��
��![]() Ϊ�ۺ������۵�������
Ϊ�ۺ������۵�������![]() ����
����![]() �����ȷֵ��ϣ���
�����ȷֵ��ϣ���![]() �ij�Ϊ�� ��
�ij��� ��

A.8B.10C.8��10D.8��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ϣ�˼����ͬѧС���ڽ�����ȵ�ʽ���⣺����֪����![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��ʱ�����������������
��ֵ��ʱ�����������������![]() �������ȵ�ʽת��Ϊ��������ʽ�������õ�ʽ�Ļ����������������ֵ.�����ó�
�������ȵ�ʽת��Ϊ��������ʽ�������õ�ʽ�Ļ����������������ֵ.�����ó�![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ���Ӷ��������.�������£�
֮��Ĺ�ϵ���Ӷ��������.�������£�
�⣻��![]() �����У�
������
![]() ��
��![]() ��
��![]() ��
��
������������ʽ��ӣ���![]() .
.
![]()
![]() ��
��![]() ��
��![]() ��������
��������
![]()
![]() ����
����![]() ��.
��.
![]()
![]() .
.
��ϸ�Ķ��������ϣ������������⣺
��1��������![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
��2����֪![]() ��
��![]() ��
��![]() ��
��![]() ������ȣ���֤��
������ȣ���֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
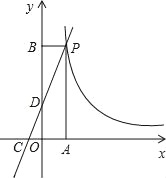
����Ŀ����ͼ��һ�κ���y=kx+2��ͼ���뷴��������y=![]() ��ͼ���ڵ�һ���Ľ���ΪP��PA��x���ڵ�A��PB��y���ڵ�B������y=kx+2��ͼ��ֱ�x�ᣬy���ڵ�C��D����֪��OCD�����S��OCD=1��
��ͼ���ڵ�һ���Ľ���ΪP��PA��x���ڵ�A��PB��y���ڵ�B������y=kx+2��ͼ��ֱ�x�ᣬy���ڵ�C��D����֪��OCD�����S��OCD=1��![]() =
=![]()
��1�����D�����ꣻ
��2����k��m��ֵ��
��3��д����x��0ʱ��ʹһ�κ���y=kx+2��ֵ���ڷ���������y=![]() ��ֵx��ȡֵ��Χ��
��ֵx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com