
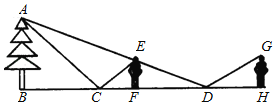
【题目】小明想用镜子测量一棵松树的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子放在D点,人在G点正好看到树尖A.已知小明的眼睛距离地面1.70m,量得CD=12m,CF=1.8m,DH=3.8m.请你求出松树的高.
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是A(-1,0)、B(4,5),抛物线![]() +b
+b![]() +c经过A、B两点
+c经过A、B两点
(1)求抛物线的解析式;
(2)点M是线段AB上的一点(不与A、B重合),过M作![]() 轴的垂线交抛物线与点N,求线段MN的最大值,并求出点M、N的坐标;
轴的垂线交抛物线与点N,求线段MN的最大值,并求出点M、N的坐标;
(3)在(2)的条件下,在抛物线上是否存在点P,使得⊿PMN是以MN为直角边的直角三角形?若存在求出点P的坐标,若不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
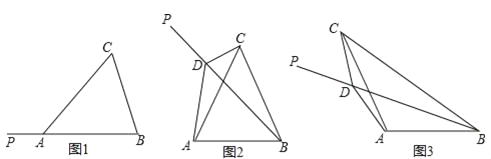
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
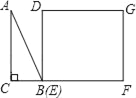
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. 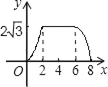 B.
B. 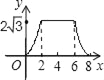 C.
C. 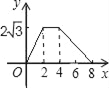 D.
D. 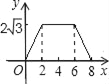
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索发现)
如图①,是一张直角三角形纸片,![]() ,小明想从中剪出一个以
,小明想从中剪出一个以![]() 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线
为内角且面积最大的矩形,经过多次操作发现,当沿着中位线![]() 、
、![]() 剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为_____________.
剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为_____________.
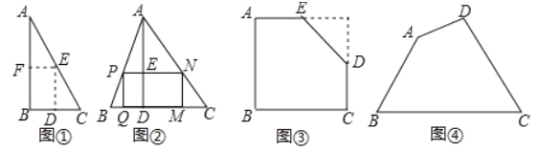
(拓展应用)
如图②,在![]() 中,
中,![]() ,
,![]() 边上的高
边上的高![]() ,矩形
,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,顶点
上,顶点![]() 、
、![]() 在边
在边![]() 上,则矩形
上,则矩形![]() 面积的最大值为_________.(用含
面积的最大值为_________.(用含![]() 的代数式表示)
的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,小明从中剪出了一个面积最大的矩形(
,小明从中剪出了一个面积最大的矩形(![]() 为所剪出矩形的内角),求该矩形的面积.
为所剪出矩形的内角),求该矩形的面积.
(实际应用)
如图④,现有一块四边形的木板余料![]() ,经测量
,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,木匠徐师傅从这块余料中裁出了顶点
,木匠徐师傅从这块余料中裁出了顶点![]() 、
、![]() 在边
在边![]() 上且面积最大的矩形
上且面积最大的矩形![]() ,求该矩形的面积.
,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在开业前,所进三种货物:上衣、裤子和鞋子的数量共480份,这三种货物进货的数量比例如图(1)所示.商店安排6人只销售上衣,4人只销售裤子,2人只销售鞋子,用了5天的时间销售货物的情况如图(2)及表格所示.
(1)求所进三种货物中上衣有多少件?
(2)直接在图中把图(2)补充完整;
(3)表格中的![]() = (直接填空);
= (直接填空);
(4)若销售人员不变,并以同样的销售速度销售,则上衣、裤子和鞋子中最先销售完的货物为 (直接填空).

货物 | 上衣(件) | 裤子(条) | 鞋子(双) |
5天的销售总额 | 150 | a | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可以旋转,当
可以旋转,当![]() 绕点
绕点![]() 逆时针旋转时,投影探头
逆时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到
.(结果精确到![]() )
)
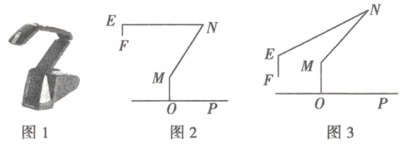
(1)如图2所示,![]() ,
,![]() .
.
①填空:![]() ;
;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离;
的距离;
(2)如图3所示,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据
的大小.(参考数据![]() span>)
span>)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克至60千克之间(含20千克和60千克)时,每千克批发5元;若超过60千克是,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:
蔬菜的批发量(千克) | ... | 25 | 60 | 75 | 90 | ... |
所付的金额(元) | ... | 125 | 300 | ... |
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量![]() (千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出
(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
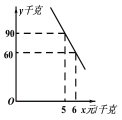
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com