
【题目】如图,已知在△ABC中,AB=AC,点D为BC上一点(不与点B、点C重合),连结AD,以AD为边在右侧作△ADE,DE交AC于点F,其中AD=AE,∠ADE=∠B.
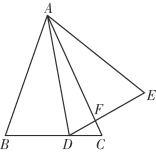
(1)求证:△ABD∽△AEF;
(2)若![]() =
=![]() ,记△ABD的面积为S1,△AEF的面积为S2,求
,记△ABD的面积为S1,△AEF的面积为S2,求![]() 的值.
的值.
 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,2),B(3,4),C(4,1),连接AB、BC、CA,平移△ABC得到△DEF,其中A点与D点对应,B点与E点对应,C点与F点对应。
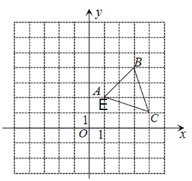
(1)使E与A重合,画出△DEF,并写出F的坐标;
(2)若将△ABC向左平移![]() 个单位,使得到的△DEF的顶点D、F分别位于
个单位,使得到的△DEF的顶点D、F分别位于![]() 轴两侧,求
轴两侧,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD和四边形CEFG都是正方形,且AB>CE

(1) 如图1,连接BG、DE,求证:BG=DE
(2) 如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD
① 求∠BDE的度数
② 若正方形ABCD的边长是![]() ,请直接写出正方形CEFG的边长____________
,请直接写出正方形CEFG的边长____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则sin∠AEC的值为( )
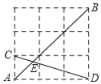
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
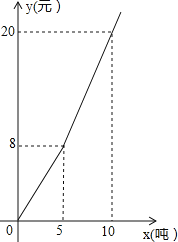
【题目】浙江实施“五水共治“以来,越来越重视节约用水,某地对居民用水按阶梯水价方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题.
(1)请写出y与x的函数关系式;
(2)若某个家庭有5人,响应节水号召,计划控制1月份的生活用水费不超过76元,则该家庭这个月最多可以用多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A. a≤﹣5B. a≥5C. a=7D. a≥7
查看答案和解析>>
科目:初中数学 来源: 题型:
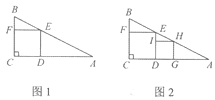
【题目】我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
(1)如图l,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是________;
(2)如图2,四边形DGHI是(1)中△EDA的内接正方形,那么第2个正方形DGHI的边长记为a2;继续在图2中的△HGA中按上述方法作第3个内接正方形……以此类推,则第n个内接正方形的边长an=____. (n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com