
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
【答案】(1) y=x2-2x-3 ;(2) 对称轴是x=1,顶点坐标(1,-4) ;(3) (1+2![]() ,4)或(1-2
,4)或(1-2![]() ,4)或(1,-4)
,4)或(1,-4)
【解析】试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得P点的坐标.
试题解析:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,
∴![]() AB|yP|=8,
AB|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2![]() ,
,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
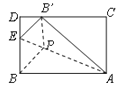
【题目】矩形纸片ABCD中,AB=3,AD=4,将纸片折叠,使点B落在边CD上的B’处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(-![]() ,y1),C(-
,y1),C(-![]() ,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
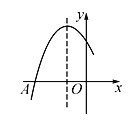
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作
y轴的平行线,与直线AC交于点G(点G在点F的上方).若, ![]()
求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ,
,![]() ,以
,以![]() 为圆心,任意长为半径画弧,分别交
为圆心,任意长为半径画弧,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,再分别以
,再分别以![]() ,
,![]() ,为圆心,大于
,为圆心,大于![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ,作弧线
,作弧线![]() ,交
,交![]() 于点
于点![]() .已知
.已知![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com