
【题目】已知四边形ABCD和四边形CEFG都是正方形,且AB>CE

(1) 如图1,连接BG、DE,求证:BG=DE
(2) 如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD
① 求∠BDE的度数
② 若正方形ABCD的边长是![]() ,请直接写出正方形CEFG的边长____________
,请直接写出正方形CEFG的边长____________
【答案】(1)见解析;(2)①∠BDE=60°;②![]() 1.
1.
【解析】
(1)根据正方形的性质可以得出BC=DC,CG=CE,∠BCD=∠GCE=90°,再证明△BCG≌△DCE就可以得出结论;
(2)①根据平行线的性质可以得出∠DCG=∠BDC=45°,可以得出∠BCG=∠BCE,可以得出△BCG≌△BCE,得出BG=BE得出△BDE为正三角形就可以得出结论;
②延长EC交BD于点H,通过证明△BCE≌△BCG就可以得出∠BEC=∠DEC,就可以得出EH⊥BD,BH=![]() BD,由勾股定理就可以求出EH的值,从而求出结论.
BD,由勾股定理就可以求出EH的值,从而求出结论.
(1)证明:∵四边形ABCD和CEFG为正方形,
∴BC=DC,CG=CE,∠BCD=∠GCE=90°.
∴∠BCD+∠DCG=∠GCE+∠DCG,
∴∠BCG=∠DCE.
在△BCG和△DCE中,
 ,
,
∴△BCG≌△DCE(SAS).
∴BG=DE;
(2)①连接BE.

由(1)可知:BG=DE.
∵CG∥BD,
∴∠DCG=∠BDC=45°.
∴∠BCG=∠BCD+∠GCD=90°+45°=135°.
∵∠GCE=90°,
∴∠BCE=360°∠BCG∠GCE=360°135°90°=135°.
∴∠BCG=∠BCE.
∵BC=BC,CG=CE,
在△BCG和△BCE中,
 ,
,
∴△BCG≌△BCE(SAS).
∴BG=BE.
∵BG=BD=DE,
∴BD=BE=DE.
∴△BDE为等边三角形。
∴∠BDE=60°.
②延长EC交BD于点H,
在△BCE和△DCE中,
 ,
,
∴△BCE≌△BCG(SSS),
∴∠BEC=∠DEC,
∴EH⊥BD,BH=![]() BD.
BD.
∵BC=CD=![]() ,在Rt△BCD中由勾股定理,得
,在Rt△BCD中由勾股定理,得
∴BD=![]() 2.
2.
∴BH=1.
∴CH=1.
在Rt△BHE中,由勾股定理,得
EH=![]() ,
,
∴CE=![]() 1.
1.
∴正方形CEFG的边长为![]() 1.
1.


科目:初中数学 来源: 题型:
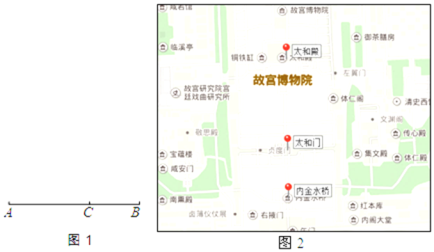
【题目】如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BCAB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在“附中博识课程中”,小白菜们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的宏伟.太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发沿相同的路线匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:①A、B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=![]() 或
或![]() .其中正确的是________(填序号).
.其中正确的是________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
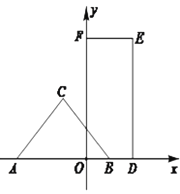
【题目】如图,等腰直角![]() 的斜边
的斜边![]() 在x轴上且长为4,点C在x轴上方.矩形
在x轴上且长为4,点C在x轴上方.矩形![]() 中,点D、F分别落在x、y轴上,边
中,点D、F分别落在x、y轴上,边![]() 长为2,
长为2,![]() 长为4,将等腰直角
长为4,将等腰直角![]() 沿x轴向右平移得等腰直角
沿x轴向右平移得等腰直角![]() .
.
(1)当点![]() 与点D重合时,求直线
与点D重合时,求直线![]() 的解析式;
的解析式;
(2)连接![]() ,
,![]() .当线段
.当线段![]() 和线段
和线段![]() 之和最短时,求矩形
之和最短时,求矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积;
重叠部分的面积;
(3)当矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积为
重叠部分的面积为![]() 时,求直线
时,求直线![]() 与y轴交点的坐标.(本问直接写出答案即可)
与y轴交点的坐标.(本问直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,点D为BC上一点(不与点B、点C重合),连结AD,以AD为边在右侧作△ADE,DE交AC于点F,其中AD=AE,∠ADE=∠B.
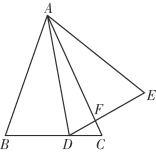
(1)求证:△ABD∽△AEF;
(2)若![]() =
=![]() ,记△ABD的面积为S1,△AEF的面积为S2,求
,记△ABD的面积为S1,△AEF的面积为S2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员徐杨在O处抛出一高球,球从离地面1m处的点A飞出,其飞行的最大高度是4m,最高处距离飞出点的水平距离是6m,且飞行的路线是抛物线一部分.以点O为坐标原点,竖直向上的方向为y轴的正方向,球飞行的水平方向为x轴的正方向建立坐标系,并把球看成一个点.(参考数据:4![]() ≈7)
≈7)

(1)求足球的飞行高度y(m)与飞行水平距离x(m)之间的函数关系式;
(2)在没有队员干扰的情况下,球飞行的最远水平距离是多少?(精确到个位)
(3)若对方一名1.7m的队员在距落点C 3m的点H处,跃起0.3m进行拦截,则这名队员能拦到球吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com