
����Ŀ����ͼ������������Ա������O���׳�һ������������1m���ĵ�A�ɳ�������е����߶���4m����ߴ�����ɳ����ˮƽ������6m���ҷ��е�·����������һ���֣��Ե�OΪ����ԭ�㣬��ֱ���ϵķ���Ϊy�������������е�ˮƽ����Ϊx���������������ϵ��������һ���㣮���ο����ݣ�4![]() ��7��
��7��

��1��������ķ��и߶�y��m�������ˮƽ����x��m��֮��ĺ�����ϵʽ��
��2����û�ж�Ա���ŵ�����£�����е���Զˮƽ�����Ƕ��٣�����ȷ����λ��
��3�����Է�һ��1.7m�Ķ�Ա�ھ����C 3m�ĵ�H����Ծ��0.3m�������أ���������Ա����������
���𰸡���1��y=��![]() ��x��6��2+4����2������е���Զˮƽ������13�ף���3��������Ա�������������ɼ�����
��x��6��2+4����2������е���Զˮƽ������13�ף���3��������Ա�������������ɼ�����
��������
��1���躯��Ϊ����ʽ���ٰѣ�0��1�����뼴����⣻
��2����y=0�������x��
��3����x=13��3=10���������ʽ���y���ٸ�1.7+0.3���бȽϼ����ж�.
��1����h=4ʱ��y=a��x��6��2+4����A��0��1��
��1=a��0��6��2+4��
��a=��![]() ��
��
��y=��![]() ��x��6��2+4��
��x��6��2+4��
��2����y=0����0=��![]() ��x��6��2+4����ã�x1=4
��x��6��2+4����ã�x1=4![]() +6��13��x2=��4
+6��13��x2=��4![]() +6��0����ȥ��
+6��0����ȥ��
������е���Զˮƽ������13�ף�
��3����x=13��3=10ʱ��y=��![]() ��10��6��2+4=
��10��6��2+4=![]() ��1.7+0.3=2��
��1.7+0.3=2��
��������Ա����������.


 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
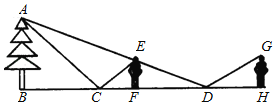
����Ŀ��С�����þ��Ӳ���һ�������ĸ߶ȣ�����������һ���ӣ����ܲ�����������֮��ľ��룬�������������þ��ӣ���ͼ��ʾ����һ�����Ѿ��ӷ���C�㣬����F��ʱ�����ھ����п�������A���ڶ��ΰѾ��ӷ���D�㣬����G�����ÿ�������A����֪С�����۾��������1.70m������CD��12m��CF��1.8m��DH��3.8m��������������ĸߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD���ı���CEFG���������Σ���AB��CE

(1) ��ͼ1������BG��DE����֤��BG��DE
(2) ��ͼ2�����������CEFG�Ƶ�C��ת��ijһλ��ǡ��ʹ��CG��BD��BG��BD
�� ���BDE�Ķ���
�� ��������ABCD�ı߳���![]() ����ֱ��д��������CEFG�ı߳�____________
����ֱ��д��������CEFG�ı߳�____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
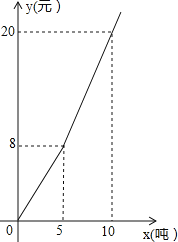
����Ŀ���㽭ʵʩ����ˮ������������Խ��Խ���ӽ�Լ��ˮ��ij�ضԾ�����ˮ������ˮ�۷�ʽ�����շѣ��˾���������ˮ�շѱ���ͼ��ʾ��ͼ��x��ʾ�˾���������ˮ�Ķ�����y��ʾ��ȡ���˾���������ˮ�ѣ�Ԫ���������ͼ����Ϣ���ش��������⣮
��1����д��y��x�ĺ�����ϵʽ��
��2����ij����ͥ��5�ˣ���Ӧ��ˮ���٣��ƻ�����1�·ݵ�������ˮ�Ѳ�����76Ԫ����ü�ͥ������������ö��ٶ�ˮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��y=x2+��1��a��x+1�ǹ���x�Ķ��κ�������x��ȡֵ��Χ��1��x��3ʱ��y��x=1ʱȡ�����ֵ����ʵ��a��ȡֵ��Χ�ǣ�������
A. a����5B. a��5C. a=7D. a��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������һ�ֶ�����б������ƻ��ӳ�����ÿ��120Ԫ�ļ۸������

��1�������г����鷢�֣���ÿ���������ۼ�Ϊ140Ԫʱ���¾�����Ϊ980�����ۼ�ÿ����10Ԫ���¾���������Ӧ����30������ʹ���ֱ������¾�����������800����ÿ�������ۼ�Ӧ�����ڶ���Ԫ��
��2����ʵ�����۹����У�����ԭ�����Ǽۺ������ɱ����ӵ�ԭ��ÿ�������Ľ���Ϊ150Ԫ����ÿ���������ۼ۱ȣ�1��������ۼۼ�����a%��a��0�����¾������ȣ�1��������¾�����800��������5a%������õ����۸ñ������¾�����ﵽ��40000Ԫ������ʵ�����۹�����ÿ�������ۼ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
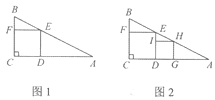
����Ŀ�����Ƕ��壺���ĸ����㶼�������α��ϵ��������������ε��ڽ���������.��֪����Rt��ABC�У���C=90����AC=6��BC=3.
��1����ͼl���ı���CDEF����ABC���ڽ������Σ���������CDEF�ı߳�a1��________��
��2����ͼ2���ı���DGHI�ǣ�1������EDA���ڽ������Σ���ô��2��������DGHI�ı߳���Ϊa2��������ͼ2�е���HGA�а�������������3���ڽ������������Դ����ƣ����n���ڽ������εı߳�an=____. ��nΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��x+m��ͼ���뷴��������y��![]() ��ͼ����A��B���㣬����x�ύ�ڵ�C����A������Ϊ��2��1����
��ͼ����A��B���㣬����x�ύ�ڵ�C����A������Ϊ��2��1����
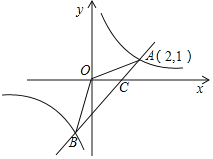
��1����m��k��ֵ��
��2�����B�����꼰��AOB�������
��3���۲�ͼ��ֱ��д��ʹ����������ֵС��һ�κ���ֵ���Ա���xȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������£�ij����ר������ij��Ʒ�Ƶ�������Ͳ���ɱ�Ϊ30Ԫ/����ÿ��������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.
��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.
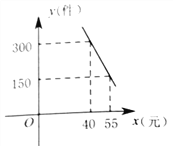
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2������涨ÿ��������Ͳ��������������240���������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
��3��������������Ĺ�����ҵ��������ÿ������������о��150Ԫ��ϣ�����̣�Ϊ�˱�֤����ÿ��ʣ��������3600Ԫ����ȷ����������Ͳ���۵��۵ķ�Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com