
【题目】等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.

(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
【答案】(1)S=![]() (t<10),
(t<10),![]() (t>10); (2)
(t>10); (2)![]() ;(3)不变,理由参见解析.
;(3)不变,理由参见解析.
【解析】
试题由题可以看出P沿AB向右运动,Q沿BC向上运动,且速度都为1cm/s,S=![]() QC×PB,所以求出QC、PB与t的关系式就可得出S与t的关系,另外应注意P点的运动轨迹,它不仅在B点左侧运动,达到一定时间后会运动到右侧,所以一些问题可能会有两种可能出现的情况,这时我们应分类回答.
QC×PB,所以求出QC、PB与t的关系式就可得出S与t的关系,另外应注意P点的运动轨迹,它不仅在B点左侧运动,达到一定时间后会运动到右侧,所以一些问题可能会有两种可能出现的情况,这时我们应分类回答.
试题解析:(1)当t<10秒时,P在线段AB上,此时CQ=t,PB=10-t
∴s=![]() ×t×(10t)=
×t×(10t)=![]() (10tt2)
(10tt2)
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t-10
∴s=![]() ×t×(t10)=
×t×(t10)=![]() (t210t)
(t210t)
(2)∵S△ABC=![]() ABBC=50
ABBC=50
∴当t<10秒时,S△PCQ=![]() (10tt2)=50
(10tt2)=50
整理得t2-10t+100=0无解
当t>10秒时,S△PCQ=![]() (t210t)="50"
(t210t)="50"
整理得t2-10t-100=0解得x=5±5![]() (舍去负值)
(舍去负值)
∴当点P运动5+5![]() 秒时,S△PCQ=S△ABC.
秒时,S△PCQ=S△ABC.
(3)当点P、Q运动时,线段DE的长度不会改变
证明:过Q作QM⊥AC,交直线AC于点M
易证△APE≌△QCM,
∴AE=PE=CM=QM=![]() t,
t,
∴四边形PEQM是平行四边形,且DE是对角线EM的一半
又∵EM=AC=10![]()
∴DE=5![]()
∴当点P、Q运动时,线段DE的长度不会改变


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类记为A;音乐类记为B;球类记为C;其他类记为D.根据调查结果发现该班每个学生都进行了等级且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
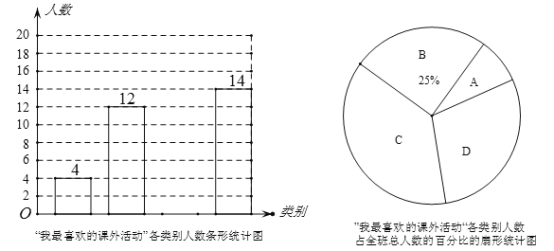
(1)七年级(1)班学生总人数为_______人,扇形统计图中D类所对应扇形的圆心角为_____度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
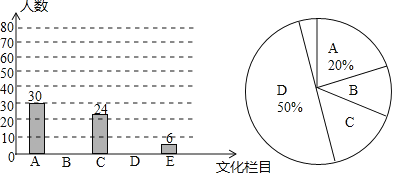
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中“B”所在扇形圆心角的度数;
(3)若选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
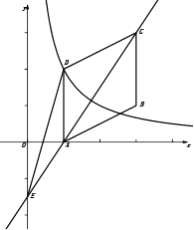
【题目】(本题满分10分)如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
(1)求此双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△ CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
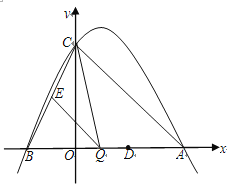
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ,当△CQE的面积为3时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,分别是两棵树及其影子的情形
(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形.
(2)请画出图中表示小丽影长的线段.
(3)阳光下小丽影子长为1.20m树的影子长为2.40m,小丽身高1.88m,求树高.

查看答案和解析>>
科目:初中数学 来源: 题型:
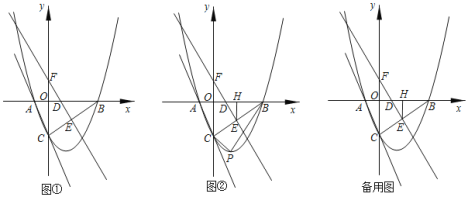
【题目】如图![]() ,在平面直角坐标系中,抛物线
,在平面直角坐标系中,抛物线![]() 分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
![]() 判定
判定![]() 的形状;
的形状;
![]() 在线段BC下方的抛物线上有一点P,当
在线段BC下方的抛物线上有一点P,当![]() 面积最大时,求点P的坐标及
面积最大时,求点P的坐标及![]() 面积的最大值;
面积的最大值;
![]() 如图
如图![]() ,过点E作
,过点E作![]() 轴于点H,将
轴于点H,将![]() 绕点E逆时针旋转一个角度
绕点E逆时针旋转一个角度![]() ,
,![]() 的两边分别交线段BO,CO于点T,点K,当
的两边分别交线段BO,CO于点T,点K,当![]() 为等腰三角形时,求此时KT的值.
为等腰三角形时,求此时KT的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com