
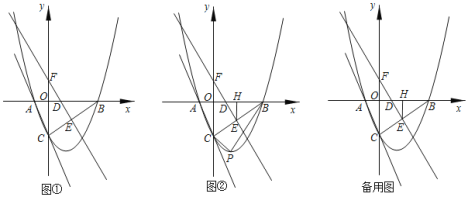
【题目】如图![]() ,在平面直角坐标系中,抛物线
,在平面直角坐标系中,抛物线![]() 分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
![]() 判定
判定![]() 的形状;
的形状;
![]() 在线段BC下方的抛物线上有一点P,当
在线段BC下方的抛物线上有一点P,当![]() 面积最大时,求点P的坐标及
面积最大时,求点P的坐标及![]() 面积的最大值;
面积的最大值;
![]() 如图
如图![]() ,过点E作
,过点E作![]() 轴于点H,将
轴于点H,将![]() 绕点E逆时针旋转一个角度
绕点E逆时针旋转一个角度![]() ,
,![]() 的两边分别交线段BO,CO于点T,点K,当
的两边分别交线段BO,CO于点T,点K,当![]() 为等腰三角形时,求此时KT的值.
为等腰三角形时,求此时KT的值.
【答案】![]() △ABC为直角三角形;
△ABC为直角三角形;![]() 当
当![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]() ,此时
,此时![]() ;
;![]() 当
当![]() 是等腰三角形时,KT的值为
是等腰三角形时,KT的值为![]() 或
或![]() .
.
【解析】
(1)结论:△ABC是直角三角形.求出A、B、C三点坐标,求出AC、BC、AB的长,利用勾股定理的逆定理证明即可.
(2)作P作PG∥y轴,交BC于G,先利用待定系数法求直线BC的解析式为:![]() ,设P(x,
,设P(x,![]() ),则G(x,
),则G(x,![]() ),根据三角形面积公式表示△BCP面积,配方可得结论;
),根据三角形面积公式表示△BCP面积,配方可得结论;
(3)①如图,当K与O重合,T与D重合时,△EKT的等腰三角形,求出KT即可解决问题.②如图,当TE=KE时,作KN⊥CE于N,EQ⊥OC于Q,则四边形OQEH是矩形,由△KEN≌△ETH,推出KN=EH=1,再想办法求出OK,OT即可解决问题.
![]() 为直角三角形,理由如下:
为直角三角形,理由如下:
当![]() 时,
时,![]() ,
,
![]() 点C的坐标为
点C的坐标为![]() ;
;
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点A的坐标为
点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() 为直角三角形.
为直角三角形.
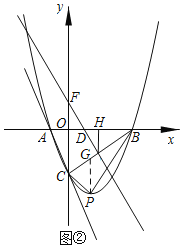
![]() 如图
如图![]() ,过P作
,过P作![]() 轴,交BC于G,
轴,交BC于G,
![]() 点B的坐标为
点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,
,
易得直线BC的解析式为:![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() 是直线BC下方抛物线上的点,
是直线BC下方抛物线上的点,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]() ,此时
,此时![]() ;
;
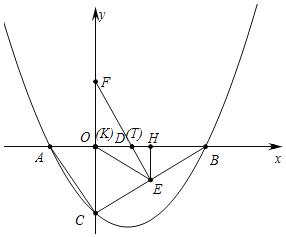
![]() 如下图中,
如下图中,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
当K与O重合,T与D重合时,![]() 是等腰三角形,
是等腰三角形,
易知![]() ,
,
![]() ,
,
![]() .
.
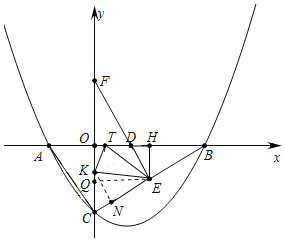
![]() 如图,当
如图,当![]() 时,作
时,作![]() 于N,
于N,![]() 于Q,则四边形OQEH是矩形,
于Q,则四边形OQEH是矩形,
易知:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 中,易知
中,易知![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
综上所述,当![]() 是等腰三角形时,KT的值为
是等腰三角形时,KT的值为![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令
,令![]() .
.
(1)若![]() 的函数图象相交于
的函数图象相交于![]() 轴上的同一点.
轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,
为何值时,![]() 的值最小,试求出该最小值.
的值最小,试求出该最小值.
(2)当![]() 时,
时,![]() 随
随![]() 的增大而减小,请写出
的增大而减小,请写出![]() 的大小关系并给予证明.
的大小关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.

(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过30 m的区域划分为A票区,B票区如图所示,剩下的为C票区.(π取3)
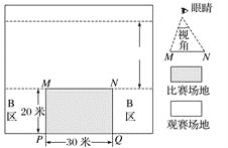
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要作出图形,保留作图痕迹,不要求写作法);
(2)如果每个座位所占的平均面积是0.8平方米,请估算A票区有多少个座位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时相向匀速行驶.当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达A地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则B,C两地相距 千米.
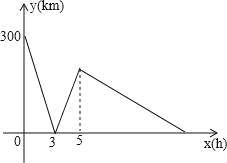
查看答案和解析>>
科目:初中数学 来源: 题型:
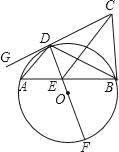
【题目】如图,⊙O的直径DF与弦AB交于点E,C为⊙O外一点,CB⊥AB,G是直线CD上一点,∠ADG=∠ABD.
求证:ADCE=DEDF;
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路过程写出来(要求至少写3步);
(2)在你经历说明(1)的过程之后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
①∠CDB=∠CEB;
②AD∥EC;
③∠DEC=∠ADF,且∠CDE=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
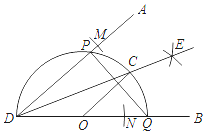
【题目】已知∠ADB,作图.
步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于![]() MN长为半径画弧交于点E,画射线DE.
MN长为半径画弧交于点E,画射线DE.
步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;
步骤3:连结PQ、OC.
则下列判断:①![]() ;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
A. ①③④ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
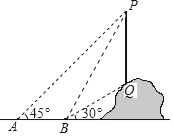
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
A. 6+2![]() B. 6+
B. 6+![]() C. 10﹣
C. 10﹣![]() D. 8+
D. 8+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com