
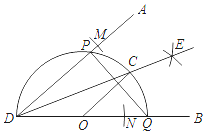
����Ŀ����֪��ADB����ͼ��
����1���Ե�DΪԲ�ģ��ʵ���Ϊ�뾶�������ֱ�DA��DB�ڵ�M��N���ٷֱ��Ե�M��NΪԲ�ģ�����![]() MN��Ϊ�뾶�������ڵ�E��������DE��
MN��Ϊ�뾶�������ڵ�E��������DE��
����2����DB����ȡһ��O���Ե�OΪԲ�ģ�OD��Ϊ�뾶����Բ���ֱ�DA��DB��DE�ڵ�P��Q��C��
����3������PQ��OC��
�������жϣ���![]() ����OC��DA����DP=PQ����OC��ֱƽ��PQ��������ȷ�Ľ����У�������
����OC��DA����DP=PQ����OC��ֱƽ��PQ��������ȷ�Ľ����У�������
A. �٢ۢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
���𰸡�B
��������
��DQΪֱ���ɵó�DA��PQ�����OC��PQ�ɵó�DA��OC����������ȷ������ͼ��֪��CDQ=��PDC�������ɵó���PC=��CQ ��OCƽ����AOB�������٢���ȷ������AOB�Ķ���δ֪�����ܵó�DP=PQ�����������������ϼ��ɵó����ۣ�
�⣺��DQΪֱ����
���DPQ=90�㣬DA��PQ��
��OC��PQ��
��DA��OC����������ȷ��
����ͼ��֪����CDQ=��PDC��
����PC=��CQ��OCƽ����AOB�������٢���ȷ��
�ߡ�ADB�Ķ���δ֪����PDQ����PQD���࣬
���PDQ��һ��������PQD��
��DP��һ������PQ������������
������������ȷ�Ľ������٢ڢܣ�
��ѡ��B��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
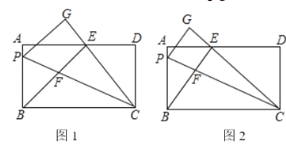
����Ŀ����ͼ1������ABCD�Ľ϶̱�CDΪһ��������CDEF,ʹ��F���ڱ�AD�ϣ�����BE����AF�ڵ�G.
��1������BG��EG��������ϵ.��˵�����ɣ�
��2���ӳ�DE,BA���ڵ�H�������������䣬
����ͼ2������ADC=60������![]() ��ֵ��
��ֵ��
����ͼ3������ADC=����0��<��<90�㣩,ֱ��д��![]() ��ֵ.���ú��������Ǻ�����ʾ��
��ֵ.���ú��������Ǻ�����ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ�����ABCD��AB��12��P�DZ�AB��һ�㣬�ѡ�PBC��ֱ��PC�۵�������B�Ķ�λ��G������B��BE��CG������ΪE����AD�ϣ�BE��PC�ڵ�F
��1����ͼ1������E��AD���е㣬��֤����AEB�ա�DEC��
��2����ͼ2������֤��BP��BF���ڵ�AD��25����AE��DEʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6�֣���ͼ����ƽ��ֱ������ϵ�У�������ÿһ��С�����εı߳�Ϊ1����λ���ȣ���֪��ABC��
��1��������ABC��OΪ��ת���ģ�˳ʱ����ת90��ġ�A1B1C1����ֻ����ͼ�Σ���
��2��������ABC����ԭ��O�����ĶԳƵġ�A2B2C2����ֻ����ͼ�Σ���д��B2��C2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����16��ʡ�˻�������¡�ؾ��У��ƶ������и�У����������ݱ�Ŀ�չ����ijУ����ӵ�һ��ѵ���У��ף��������˶�Աǰ5����ƽ���ɼ���ͬ�����������˵ijɼ����Ƴ������в�������ͳ��ͼ��.
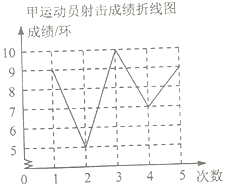
���˶�Ա�ɼ�ͳ�Ʊ�(��λ����)
��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
8 | 10 | 8 | 6 |
|
(1)���˶�Աǰ5������ɼ��������� ������λ���� ����
(2)�����˶�Ա��5�εijɼ���
(3)�������ѡ��һ���ɼ��ȶ����˶�Ա�μ�ȫ����ѧ������������ΪӦѡ˭ȥ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�꼶380��ʦ�����Σ��ƻ�����7���ͳ������мס��������ͺſͳ������ǵ��ؿ�������������
���ֿͳ� | ���ֿͳ� | |
�ؿ�������/���� | 60 | 45 |
���Ԫ/���� | 550 | 450 |
��1�������ü��ֿͳ�x������ܷ���ΪyԪ�����y��Ԫ����x������֮��ĺ�������ʽ��
��2�������ֿͳ��ж�����ʱ���ܱ������е�ʦ���ܲμ���������������٣����ٷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������壩
���ı��ε�һ���Խ����ܽ��ı��ηָ���������Ƶ�ֱ�������Σ���ô���ǽ������ı��ν�������Ծ�ı��Ρ��������Խ��߽�������Ծ�ߡ���
��������
��1�����⡰���Ǿ��ζ�����Ծ�ı��Ρ���ʲô���⣨���桱�١�����
��2���ı���ABCDΪ����Ծ�ı��Ρ����ҶԽ���ACΪ����Ծ�ߡ�������AC��CB����B=30�㣬AB=4![]() �����ı���ABCD���ܳ���
�����ı���ABCD���ܳ���
��ʵ��Ӧ�ã���֪������y=ax2+m��a��0����x�ύ��B����2��0����C���㣬��ֱ��y=2x+b����A��B���㣮
��3��ֱ��д��C�����꣬����������ߵĽ���ʽ��
��4�����߶�AB����һ����P��������BC����һ����Q��P��Q����ֱ���![]() ����λ/�룬5����λ/����ٶ�ͬʱ��B��������BA��BC�����˶������˶�ʱ��Ϊt��������һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶����ڵ�һ�������������Ƿ���ڵ�M��ʹ���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı��Ρ��������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
����λ/�룬5����λ/����ٶ�ͬʱ��B��������BA��BC�����˶������˶�ʱ��Ϊt��������һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶����ڵ�һ�������������Ƿ���ڵ�M��ʹ���ı���BQMP����PQΪ����Ծ�ߡ��ġ���Ծ�ı��Ρ��������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
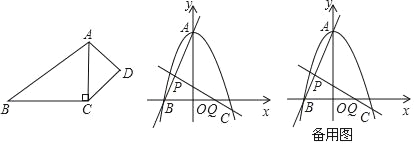
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������һ���ߵ�ƽ�������������ߵij˻������ǰ���������ν������������Σ�

![]() ��֪
��֪![]() �DZ��������Σ�
�DZ���������![]() ��
��![]() ����ֱ��д����������������AC�ij���
����ֱ��д����������������AC�ij���
![]() ��ͼ1�����ı���ABCD�У�
��ͼ1�����ı���ABCD�У�![]() ���Խ���BDƽ��
���Խ���BDƽ��![]() ��
��![]() ��֤��
��֤��![]() �DZ��������Σ�
�DZ���������
![]() ��ͼ2����
��ͼ2����![]() �������£���
�������£���![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com