
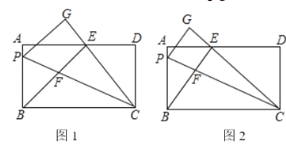
【题目】在矩形中ABCD,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对位点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,①求证:BP=BF;②当AD=25,且AE<DE时,求![]() 的值.
的值.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
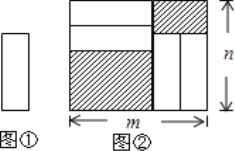
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.

(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 ;
(2)抽查C厂家的合格零件为 件,并将图1补充完整;
(3)通过计算说明合格率排在前两名的是哪两个厂家.
查看答案和解析>>
科目:初中数学 来源: 题型:
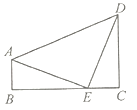
【题目】已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b, 请写出求tan∠ADB的思路.(不用写出计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.
(1)依题意补全图形;
(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);
(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1876年,美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理,若图中![]() ,
,![]() ,
,![]() ,则下面结论错误的是( )
,则下面结论错误的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 是等腰直角三角形
是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
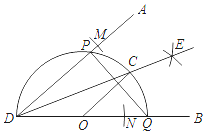
【题目】已知∠ADB,作图.
步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于![]() MN长为半径画弧交于点E,画射线DE.
MN长为半径画弧交于点E,画射线DE.
步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;
步骤3:连结PQ、OC.
则下列判断:①![]() ;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
A. ①③④ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
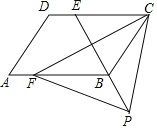
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )
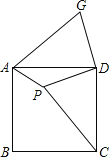
A.150°B.135°C.120°D.108°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com