
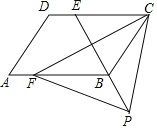
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.
(1)依题意补全图形;
(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);
(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
相交于点A(m,6)和点B(﹣3,n),直线AB与y轴交于点C.
(1)求直线AB的表达式;
(2)求AC:CB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
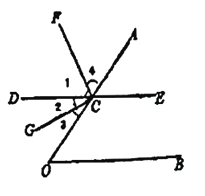
【题目】推理填空:如图,点![]() 在
在![]() 的一边
的一边![]() 上,过点
上,过点![]() 的直线
的直线![]() 平行直线
平行直线![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)当![]() 为多少度时,
为多少度时,![]() 平分
平分![]() ,并说明理由。
,并说明理由。
(1)证明:∵![]() (已知)
(已知)
∴![]() (垂直定义)
(垂直定义)
即![]()
又∵![]() (平角定义)
(平角定义)
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() (角平分线定义)
(角平分线定义)
∴![]() (_____________________)
(_____________________)
即![]() 平分
平分![]() ;
;
(2)解:![]() 时,
时,![]() 平分
平分![]() ,理由如下:
,理由如下:
∵![]() ,
,
∴![]() (____________________________),
(____________________________),
∴![]() _________________°
_________________°
又∵![]() 平分
平分![]() ,
,
∴![]() °,
°,
∴![]() (等量代换)
(等量代换)
即![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 交
交![]() 轴于点
轴于点![]() 、点
、点![]() ,交
,交![]() 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点![]() 异于
异于![]() ,且
,且![]() 在对称轴右侧),直线
在对称轴右侧),直线![]() 交对称轴于N,
交对称轴于N,
直线BE交对称轴于![]() ,对称轴交
,对称轴交![]() 轴于
轴于![]() ,试确定
,试确定![]() 、
、![]() 的数量关系并说明理由.
的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某初中为了创建书香校园,购进了一批图书.其中的20本某种科普书和30本某种文学书共花了1080元,经了解,购买的科普书的单价比文学书的单价多4元.
(1)购买的科普书和文学书的单价各多少元?
(2)另一所学校打算用800元购买这两种图书,问购进25本文学书后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:
①甲的速度为5米/秒;②100秒时甲追上乙;③经过50秒时甲乙相距50米;④甲到终点时,乙距离终点300米.其中正确的说法有( )

A. 4个 B. 3个
C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.
(1)求AB的长;
(2)求⊙O的半径.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923086297137152/1923946164551680/STEM/edc8c851f08548f08f9e61b4dab2d43e.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com