
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
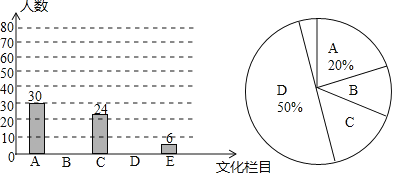
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中“B”所在扇形圆心角的度数;
(3)若选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.
【答案】(1)共调查了150名学生;(2)补图见解析;扇形统计图中“B”所在扇形圆心角的度数为36°;(3)![]() .
.
【解析】(1)由A栏目人数及其所占百分比可得总人数;
(2)总人数乘以D栏目所占百分比求得其人数,再用总人数减去其他栏目人数求得B的人数即可补全图形,用360°乘以B人数所占比例可得;
(3)列表得出所有等可能结果,然后利用概率的计算公式即可求解
(1)30÷20%=150(人),
∴共调查了150名学生.
(2)D:50%×150=75(人),B:150﹣30﹣75﹣24﹣6=15(人)
补全条形图如图所示.

扇形统计图中“B”所在扇形圆心角的度数为![]() ×360°=36°;
×360°=36°;
(3)记选择“E”的同学中的2名女生分别为N1,N2,4名男生分别为M1,M2,M3,M4,
列表如下:
N1 | N2 | M1 | M2 | M3 | M4 | |
N1 | (N1,N2) | (N1,M1) | (N1,M2) | (N1,M3) | (N1,M4) | |
N2 | (N2,N1) | (N2,M1) | (N2,M2) | (N2,M3) | (N2,M4) | |
M1 | (M1,N1) | (M1,N2) | (M1,M2) | (M1,M3) | (M1M4) | |
M2 | (M2,N1) | (M2,N2) | (M2,M1) | (M2,M3) | (M2,M4) | |
M3 | (M3,N1) | (M3,N2) | (M3,M1) | (M3,M2) | (M3,M4) | |
M4 | (M4,N1) | (M4,N2) | (M4,M1) | (M4,M2) | (M4,M3) |
∵共有30种等可能的结果,其中,恰好是同性别学生(记为事件F)的有14种情况,
∴P(F)=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点![]() 点M不与B,C重合
点M不与B,C重合![]() ,
,![]() ,CN与AB交于点N,连接OM,ON,
,CN与AB交于点N,连接OM,ON,![]() 下列五个结论:
下列五个结论:![]() ≌
≌![]() ;
;![]() ≌
≌![]() ;
;![]() ∽
∽![]() ;
;![]() ;
;![]() 若
若![]() ,则
,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()
![]()

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令
,令![]() .
.
(1)若![]() 的函数图象相交于
的函数图象相交于![]() 轴上的同一点.
轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,
为何值时,![]() 的值最小,试求出该最小值.
的值最小,试求出该最小值.
(2)当![]() 时,
时,![]() 随
随![]() 的增大而减小,请写出
的增大而减小,请写出![]() 的大小关系并给予证明.
的大小关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束. 在整个运动过程中,点C运动的路程是( )
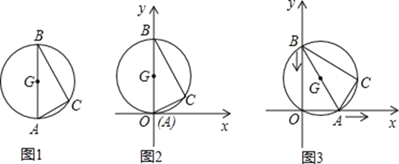
A. 4 B. 6 C. 4![]() ﹣2 D. 10﹣4
﹣2 D. 10﹣4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
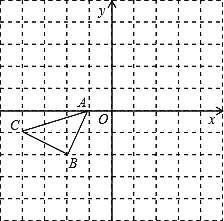
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P.若点P向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【题型】解答题
【结束】
16
【题目】《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.

(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com