
【题目】观察下列各式:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)根据你观察、归纳、发现的规律,写出![]() 可以是______的平方.
可以是______的平方.
(2)试猜想写出第![]() 个等式,并说明成立的理由.
个等式,并说明成立的理由.
(3)利用前面的规律,将![]() 改成完全平方的形式为:______.
改成完全平方的形式为:______.
【答案】(1)4025;(2)![]() ,见解析;(3)
,见解析;(3)![]() .
.
【解析】
(1)根据已知的三个等式,发现规律:等式左边是序号数与比序号数大1的两个正整数积的4倍与1的和,等式右边是序号数与比序号数大1的两个正整数的和的平方,由此得出4×2012×2013+1可以看成2012与2013这两个正整数的和的平方;
(2)猜想第n个等式为4n(n+1)+1=(n+n+1)![]() =(2n+1)
=(2n+1)![]() ,运用多项式的乘法法则计算验证即可;
,运用多项式的乘法法则计算验证即可;
(3)利用前面的规律,可知![]() =
=![]()
(1)根据观察、归纳、发现的规律,得到4×2012×2013+1=(2012+2013)![]() =4025
=4025![]() ;
;
(2)猜想第n个等式为4n(n+1)+1=(2n+1)![]() ,理由如下:
,理由如下:
∵左边=4n(n+1)+1=4n![]() +4n+1,右边=(2n+1)
+4n+1,右边=(2n+1)![]() =4n
=4n![]() +4n+1,
+4n+1,
∴左边=右边,
∴4n(n+1)+1=(2n+1)![]() ;
;
(3)利用前面的规律,可知
![]() 即
即![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三个点![]() ,
,![]() 是
是![]() 的边
的边![]() 上一点,
上一点,![]() 经平移后得到
经平移后得到![]() ,点
,点![]() 的对应点为
的对应点为![]() .
.
(1)画出平移后的![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(2)![]() 的面积为_________________;
的面积为_________________;
(3)若点![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的关系式(用含
之间的关系式(用含![]() 的式子表示
的式子表示![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
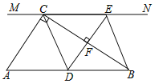
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一动点(不与
边上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当![]() 移动到
移动到![]() 的什么位置时,四边形
的什么位置时,四边形![]() 是菱形?说明你的理由;
是菱形?说明你的理由;
(3)若点![]() 移动到
移动到![]() 中点,则当
中点,则当![]() 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形![]() 是正方形?请说明你的理由.
是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
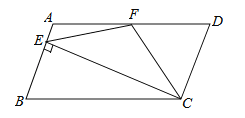
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.
A. ①②③④ B. ①②③ C. ①② D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,二元一次方程的解可以转化为点的坐标,其中x的值对应为点的横坐标,y的值对应为点的纵坐标,如二元一次方程x2y=0的解![]() 和
和![]() 可以转化为点的坐标A(0,0)和B(2,1).以方程x2y=0的解为坐标的点的全体叫做方程x2y=0的图象。
可以转化为点的坐标A(0,0)和B(2,1).以方程x2y=0的解为坐标的点的全体叫做方程x2y=0的图象。

(1)写出二元一次方程x2y=0的任意一组解___,并把它转化为点C的坐标___;
(2)在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,如方程x2y=0的图象是由该方程所有的解转化成的点组成,在图中描出点A. 点B和点C,观察它们是否在同一直线上;
(3)取满足二元一次方程x+y=3的两个解,并把它们转化成点的坐标,画出二元一次方程x+y=3的图象;
(4)根据图象,写出二元一次方程x2y=0的图象和二元一次方程x+y=3的图象的交点坐标___,由此可得二元一次方程组![]() 的解是___.
的解是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
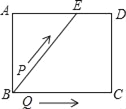
【题目】如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
A. 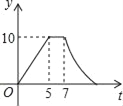 B.
B.  C.
C. 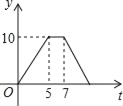 D.
D. 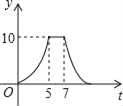
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com