
【题目】如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?

【答案】解:(1)能看到,理由如下:
由题意得,∠DFG=90°﹣53°=37°,则![]() =tan∠DFG。
=tan∠DFG。
∵DF=4米,∴DG=4×tan37°=4×0.75=3(米)。
∵老鼠躲藏处M(点M在DE上)距D点3米,∴猫头鹰能看到这只老鼠。
(2)由(1)得,AG=AD+DG=2.7+3=5.7(米),
又![]() =sin∠C=sin37°,则CG=
=sin∠C=sin37°,则CG=![]() (米)。
(米)。
答:要捕捉到这只老鼠,猫头鹰至少要飞9.5米。
【解析】试题分析:(1)根据猫头鹰从C点观测F点的俯角为53°,可知∠DFG=90°﹣53°=37°,在△DFG中,已知DF的长度,求出DG的长度,若DG>3,则看不见老鼠,若DG<3,则可以看见老鼠。
(2)根据(1)求出的DG长度,求出AG的长度,然后在Rt△CAG中,根据![]() =sin∠C=sin37°,即可求出CG的长度。
=sin∠C=sin37°,即可求出CG的长度。


科目:初中数学 来源: 题型:
【题目】已知三条不同的直线a,b,c在同一平面内,下列四个命题: ①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中正确的是 . (填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若两个数互为相反数,则它们的商为﹣1
B.一个数的绝对值一定不小于这个数
C.若两个数互为相反数,则这两个数一定是一个正数,一个负数
D.一个正数一定大于它的倒数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查,适合普查的有____,适合抽样调查的有____.(填序号)
①调查某班学生的年龄状况;②考察一个池塘里鱼的数目;③了解一批灯泡的使用寿命;④消防队调查商场的安全通道是否畅通.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】耐心算一算(同学们,请你注意解题格式,一定要写出解题步骤哦!
(1)﹣20+(﹣14)﹣(﹣18)﹣13
(2)![]()
(3)﹣24﹣ ![]() ×[5﹣(﹣3)2].
×[5﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴. 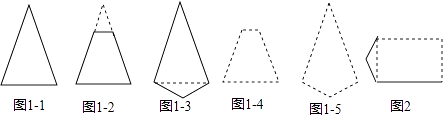
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com