练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．若$\frac{x}{y}$=$\frac{4}{5}$，则$\frac{2x-y}{x+y}$的值为（　　）
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．1D．$\frac{3}{2}$

    分析 根据等式的性质，可用x表示y，根据分式的性质，可得答案．

    解答 解：由$\frac{x}{y}$=$\frac{4}{5}$，得
    y=$\frac{5}{4}$x．
    $\frac{2x-y}{x+y}$=$\frac{2x-\frac{5}{4}x}{x+\frac{5}{4}x}$=$\frac{\frac{3}{4}x}{\frac{9}{4}x}$=$\frac{1}{3}$，
    故选：A．

    点评 本题考查了比例的性质，利用等式的性质得出y=$\frac{5}{4}$x是解题关键，又利用了分式的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    1．若一次函数y=kx+2的图象经过点（3，5），则k的值为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．两个相似多边形相似比为1：2，且它们的周长和为90，则这两个相似多边形的周长分别是30，60．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

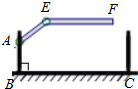    19．某地下车库出口处安装了“两段式栏杆”，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图所示的位置，其中AB⊥BC，EF∥BC，∠AEF=135°，AB=AE=1.3米，那么适合该地下车库的车辆限高标志牌为（栏杆宽度忽略不计．参考数据：$\sqrt{2}$≈1.4）（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

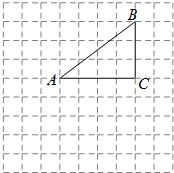    6．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上．将△ABC绕点A顺时针旋转90°得到△AB1C1．
    （1）在网格中画出△AB1C1；
    （2）计算点B旋转到B1的过程中所经过的路径长．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

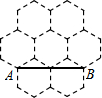    16．如图是由7个形状、大小完全相同的正六边形组成的网格，正六边形的各顶点称为格点，直角△ABC的顶点均在格点上，则满足条件的点C有（　　）
    A．6个B．8个C．10个D．12个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．在一个不透明的口袋中，放有三个标号分别为1，2，3的质地、大小都相同的小球．任意摸出一个小球，记为x，再从剩余的球中任意摸出一个小球，又记为y，得到点（x，y）．
    （1）用画树状图或列表等方法求出点（x，y）的所有可能情况；
    （2）求点（x，y）在二次函数y=ax2-4ax+c（a≠0）图象的对称轴上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图1，在△ABC中，AB=AC，G为三角形外一点，且△GBC为等边三角形．
    （1）求证：直线AG垂直平分BC；
    （2）以AB为一边作等边△ABE（如图2），连接EG、EC，试判断△EGC是否构成直角三角形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

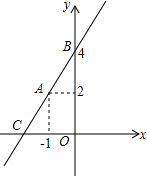    1．如图，一次函数的图象经过平面直角坐标系中A、B两点．
    （1）求一次函数解析式；
    （2）当x=5时，求y的值；
    （3）求一次函数图象与坐标轴围成的△BOC的面积．

    查看答案和解析>>

    同步练习册答案