
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() .
.
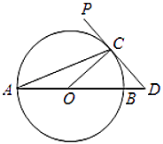
(1)求![]() 的度数.
的度数.
(2)若![]() 的半径为2,求
的半径为2,求![]() 的长.
的长.
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
(1)当⊙O的半径为2时,
①如果点A(0,1),B(3,4),那么d(A,⊙O)=_______,d(B,⊙O)= ________;
②如果直线![]() 与⊙O互为“可及图形”,求b的取值范围;
与⊙O互为“可及图形”,求b的取值范围;
(2)⊙G的圆心G在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
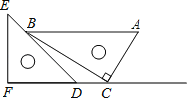
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有完全相同的三个小球,把它们分别标号为1,2,3. 小林和小华做一个游戏,按照以下方式抽取小球:先从布袋中随机抽取一个小球,记下标号后放回布袋中搅匀,再从布袋中随机抽取一个小球, 记下标号. 若两次抽取的小球标号之和为奇数,小林赢;若标号之和为偶数,则小华赢.
(1)用画树状图或列表的方法,列出前后两次取出小球上所标数字的所有可能情况;
(2)请判断这个游戏是否公平,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏打算在某外卖网站点如下表所示的菜品和米饭.已知每份订单的配送费为3元,商家为促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元.如果小敏在购买下表的所有菜品和米饭时,采取适当的下单方式,那么他的总费用最低可为( )
菜品 | 单价(含包装费) | 数量 | |
| 水煮牛肉(小) | 30元 | 1 |
| 醋溜土豆丝(小) | 12元 | 1 |
| 豉汁排骨(小) | 30元 | 1 |
| 手撕包菜(小) | 12元 | 1 |
| 米饭 | 3元 | 2 |
A.48元B.51元C.54元D.59元
查看答案和解析>>
科目:初中数学 来源: 题型:
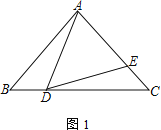
【题目】已知:△ABC中,点D为边BC上一点,点E在边AC上,且∠ADE=∠B
(1) 如图1,若AB=AC,求证:![]() ;
;
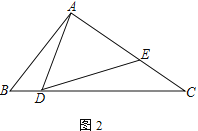
(2) 如图2,若AD=AE,求证:![]() ;
;
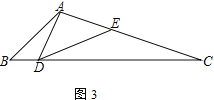
(3) 在(2)的条件下,若∠DAC=90°,且CE=4,tan∠BAD=![]() ,则AB=____________.
,则AB=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
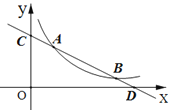
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;
(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂拟建一个如图所示的矩形仓库ABCD,仓库的一边是长为12m的一面墙,另外三边用30m长的建筑材料围成.设AB的长为xm,矩形ABCI的面积为Sm2.
(1)用含x的代数式表示BC的长,并求出x的取值范围.
(2)写出S关于x的函数关系式,并求出S的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com