

分析 (1)由直角三角形30°角所对的边等于斜边的一半得到BD=2x,CD=4-2x,根据等角的余角相等得到∠1=∠2=30°,进而CF=2-x,可得y=4-CF=x+2;
(2)由(0,2)、(2,4)两点在y=x+2上,结合0<x<2可画出函数图象;
解答 解:(1)∵△ABC是边长等于4的等边三角形,
∴∠B=∠C=60°,AB=BC=CA=4,
∵MD⊥AB于E,∴∠1=30°.
∵BE的长为x,∴BD=2x,
∴DC=4-2x,
∵DK为法线,∴KD⊥BC,∠3和∠4分别为入射角和反射角,
∴∠3=∠4,
∴∠1=∠2=30°.
∴∠DFC=90°.
∴FC=2-x,
∴AF=4-(2-x)=x+2=y.
∴y 和 x 之间的函数关系式是 y=x+2,
自变量 x 的取值范围是 0<x<2.
(2)函数图象如下:
点评 本题考查了等边三角形的性质、直角三角形30°角所对的直角边等于斜边的一半的性质等,有一定综合性,属中档题.


科目:初中数学 来源: 题型:解答题
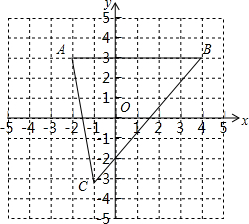 如图,已知A(-2,3)、B(4,3)、C(-1,-3).
如图,已知A(-2,3)、B(4,3)、C(-1,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,现有下列4个亊项:
如图所示,现有下列4个亊项:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全国七年级学生的视力情况 | B. | 对乘坐高铁的乘客进行安检 | ||
| C. | 了解一批电视机的使用寿命 | D. | 检测汾河某段水域的水质情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com