练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    高一新生入学军训射击训练中，小张同学的射击成绩（单位：环）为：5、7、9、10、7，则这组数据的众数是　


    7　．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


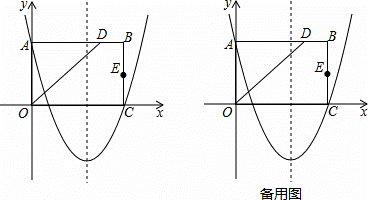
    如图，在平面直角坐标系中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，∠AOC的平分线交AB于点D，E为BC的中点，已知A（0，4）、C（5，0），二次函数y=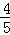x2+bx+c的图象抛物线经过A，C两点．

    （1）求该二次函数的表达式；

    （2）F、G分别为x轴，y轴上的动点，顺次连接D、E、F、G构成四边形DEFG，求四边形DEFG周长的最小值；

    （3）抛物线上是否在点P，使△ODP的面积为12？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知扇形的圆心角为120°，弧长为6π，则扇形的面积是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


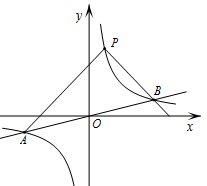
    如图，反比例函数y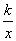＝的图像与一次函数y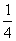＝x的图像交于点A、B，点B的横坐标是4．点P是第一象限内反比例函数图像上的动点，且在直线AB的上方．

    ⑴若点P的坐标是（1，4），直接写出k的值和△PAB的面积；

    ⑵设直线PA、PB与x轴分别交于点M、N，求证：△PMN是等腰三角形；

    ⑶设点Q是反比例函数图像上位于P、B之间的动点（与点P、B不重合），连接AQ、BQ，比较∠PAQ与∠PBQ的大小，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，四边形ABCD是⊙O的内接四边形，若∠DAB=60°，则∠BCD的度数是（　　）

    　

    A．

    60°

    B．

    90°

    C．

    100°

    D．

    120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式组：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读材料：用配方法求最值．

    已知x，y为非负实数，

    ∵x+y﹣2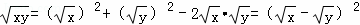≥0

    ∴x+y≥2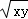，当且仅当“x=y”时，等号成立．

    示例：当x＞0时，求y=x+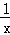+4的最小值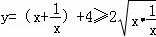．+4=6，当x=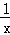，即x=1时，y的最小值为6．

    （1）尝试：当x＞0时，求y=的最小值．

    （2）问题解决：随着人们生活水平的快速提高，小轿车已成为越来越多家庭的交通工具，假设某种小轿车的购车费用为10万元，每年应缴保险费等各类费用共计0.4万元，n年的保养、维护费用总和为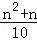万元．问这种小轿车使用多少年报废最合算（即：使用多少年的年平均费用最少，年平均费用=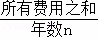）？最少年平均费用为多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知E、F、G、H分别为菱形ABCD四边的中点，AB=6cm，∠ABC=60°，则四边形EFGH的面积为　　cm2．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    函数y=x﹣2的图象不经过（　　）

    　

    A．

    第一象限

    B．

    第二象限

    C．

    第三象限

    D．

    第四象限

    查看答案和解析>>

    同步练习册答案