
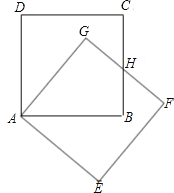
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下列程序计算,把答案填写在表格里,然后看看有什么规律,想想为什么会有
这个规律?
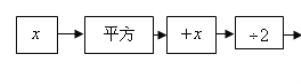
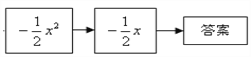
(1)填写表内空格:
输入 | 3 | 2 | -2 |
| … |
输出答案 | 0 | … |
(2)你发现的规律是____________.
(3)用简要过程说明你发现的规律的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
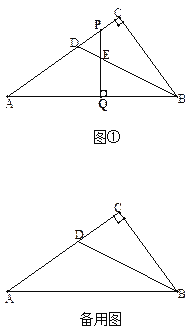
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组进行了如下探究:(1)如图①,若四边形ABCD是矩形,对角线AC、BD交点为P,过点P作PQ⊥BC于点Q,连结DQ交AC于点P1,过点P1作P1Q1⊥BC于点Q1,已知AB=CD=a,则PQ= ,P1Q1= .(用含a的代数式表示)
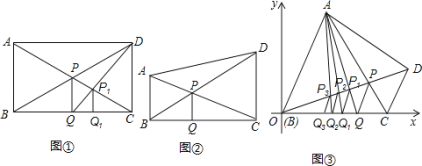
(2)如图②,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AC、BD交于点P,过点P作PQ⊥BC于点Q.已知AB=a,CD=b,请用含a、b的代数式表示线段PQ的长,写出你的解题过程.
(3)如图③,在直角坐标系xOy中,梯形ABCD的腰BC在x轴正半轴上(点B与原点O重合),AB∥CD,∠ABC=60°,AC、BD交于点P,过点P作PQ∥CD交BC于点Q,连结AQ交BD于点P1,过点P1作P1Q1∥CD交BC于点Q1.连结AQ1交BD于点P2,过点P2作P2Q2∥CD交BC于点Q2,…,已知AB=a,CD=b,则点P1的纵坐标为 点Pn的纵坐标为 (直接用含a、b、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△A′B′C′中,有下列条件:①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠B′;⑥∠C=∠C′,则以下各组条件中不能保证△ABC≌△A′B′C′的一组是( )
A. ①②③B. ①②⑤C. ①③⑤D. ②⑤⑥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com