
【题目】某班数学兴趣小组进行了如下探究:(1)如图①,若四边形ABCD是矩形,对角线AC、BD交点为P,过点P作PQ⊥BC于点Q,连结DQ交AC于点P1,过点P1作P1Q1⊥BC于点Q1,已知AB=CD=a,则PQ= ,P1Q1= .(用含a的代数式表示)
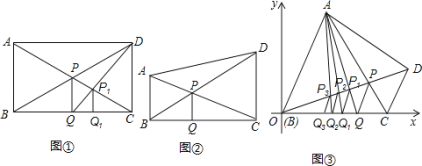
(2)如图②,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AC、BD交于点P,过点P作PQ⊥BC于点Q.已知AB=a,CD=b,请用含a、b的代数式表示线段PQ的长,写出你的解题过程.
(3)如图③,在直角坐标系xOy中,梯形ABCD的腰BC在x轴正半轴上(点B与原点O重合),AB∥CD,∠ABC=60°,AC、BD交于点P,过点P作PQ∥CD交BC于点Q,连结AQ交BD于点P1,过点P1作P1Q1∥CD交BC于点Q1.连结AQ1交BD于点P2,过点P2作P2Q2∥CD交BC于点Q2,…,已知AB=a,CD=b,则点P1的纵坐标为 点Pn的纵坐标为 (直接用含a、b、n的代数式表示)
【答案】(1)![]() a;
a;![]() a;(2)
a;(2)![]() ;(3)
;(3)![]() ;
;![]() .
.
【解析】
试题分析:(1)根据矩形的对角线互相平分且相等可得BP=PD,再根据在同一平面内,垂直于同一直线的两直线互相平行可得PQ∥CD,然后根据平行线分线段成比例定理列式求解即可得到PQ,同理求出P1Q1∥CD,然后求出![]() 的值,再求出
的值,再求出![]() 的值,然后根据平行线分线段成比例定理可得
的值,然后根据平行线分线段成比例定理可得![]() ,再代入数据进行计算即可求出P1Q1;
,再代入数据进行计算即可求出P1Q1;
(2)先根据AB∥CD求出![]() ,然后求出
,然后求出![]() ,再根据在同一平面内,垂直于同一直线的两直线互相平行可得PQ∥CD,然后根据平行线分线段成比例定理可得
,再根据在同一平面内,垂直于同一直线的两直线互相平行可得PQ∥CD,然后根据平行线分线段成比例定理可得![]() ,代入数据进行计算即可得解;
,代入数据进行计算即可得解;
(3)根据(2)的结论依次表示出PQ、P1Q1、P2Q2…PnQn,再根据两直线平行,同位角相等求出∠PQC=∠P1Q1C=∠P2Q2C=…∠PnQnC=∠ABC=60°,然后利用60°角的正弦值列式计算即可得解.
试题解析:(1)∵四边形ABCD是矩形,
∴BP=PD,
∵PQ⊥BC,
∴PQ∥CD,
∴![]() ,
,
∴PQ=![]() CD=
CD=![]() a,
a,
∵P1Q1⊥BC,
∴P1Q1∥CD,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴P1Q1=![]() a;
a;
(2)∵AB∥CD,
∴![]() ,
,
∴![]() ,
,
∵AB∥CD,∠ABC=90°,PQ⊥BC,
∴PQ∥CD,
∴![]() ,
,
∴PQ=![]() ;
;
(3)根据(2)的结论,PQ=![]() ,
,
P1Q1=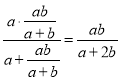 ,
,
P2Q2= ,
,
P3Q3= ,
,
…,
依此类推,PnQn=![]() ,
,
∵AB∥CD,PQ∥CD,P1Q1∥CD,P2Q2∥CD,…,
∴AB∥PQ∥P1Q1∥P2Q2∥…∥PnQn∥CD,
∴∠PQC=∠P1Q1C=∠P2Q2C=…∠PnQnC=∠ABC=60°,
∴点P1的纵坐标为:P1Q1![]() sin60°=
sin60°=![]() ,
,
点Pn的纵坐标为为PnQn![]() sin60°=
sin60°=![]() .
.


科目:初中数学 来源: 题型:
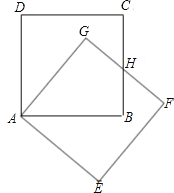
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.

(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ;
(2)若两个三角形面积满足S△POQ=![]() S△PAQ,求m的值;
S△PAQ,求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD![]() DQ的最大值.
DQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com