
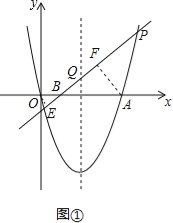
【题目】如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.

(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ;
(2)若两个三角形面积满足S△POQ=![]() S△PAQ,求m的值;
S△PAQ,求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD![]() DQ的最大值.
DQ的最大值.
【答案】(1)x=2,45;(2)m=-1或2;(3)①6![]() ;②18.
;②18.
【解析】试题分析:(1)把解析式转化成顶点式,或利用对称轴公式即可得该抛物线的对称轴,利用直线y=x+m与坐标轴的交点坐标即可求得直线PQ与x轴所夹锐角的度数;(2)分情况讨论,即直线PQ与x轴的交点落在OA的延长线上,OA上,AO的延长线上三种情况讨论m值.设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,,当点B在OA的延长线时,S△POQ=![]() S△PAQ不成立;当点B落在线段OA上时,
S△PAQ不成立;当点B落在线段OA上时, ![]() ,由△OBE∽△ABF得,
,由△OBE∽△ABF得, ![]() ,由对称轴求出A点坐标,再由比例式求出B点坐标,代入直线PQ解析式,即可求得m值;当点B落在线段AO的延长线上时,同理由比例式求出B点坐标,进而确定m值;(3)①由题意可过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,AD⊥PH,DQ=DH,PD+DQ=PH,过P点作PM⊥CH于点M,可得△PMH是等腰直角三角形,PH=
,由对称轴求出A点坐标,再由比例式求出B点坐标,代入直线PQ解析式,即可求得m值;当点B落在线段AO的延长线上时,同理由比例式求出B点坐标,进而确定m值;(3)①由题意可过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,AD⊥PH,DQ=DH,PD+DQ=PH,过P点作PM⊥CH于点M,可得△PMH是等腰直角三角形,PH=![]() PM,即当PM最大时,PH最大,显然当点P在抛物线顶点处时,PM最大,此时PM=6,于是求得PH的最大值.即PD+DQ的最大值;②上题求得PD+DQ的最大值为6
PM,即当PM最大时,PH最大,显然当点P在抛物线顶点处时,PM最大,此时PM=6,于是求得PH的最大值.即PD+DQ的最大值;②上题求得PD+DQ的最大值为6![]() .即PD+DQ ≤6
.即PD+DQ ≤6![]() ,设PD=a,则DQ ≤6
,设PD=a,则DQ ≤6![]() -a,所以PD
-a,所以PD![]() DQ≤a(6
DQ≤a(6![]() -a)=-(a-3
-a)=-(a-3![]() )2+18,即当PD=DQ=3
)2+18,即当PD=DQ=3![]() 时求得PD
时求得PD![]() DQ的最大值
DQ的最大值
试题解析:(1)∵y=x2-4x=(x-2)2-4,∴抛物线的对称轴是直线x=2,∵直线y=x+m与坐标轴的交点坐标为(-m,0),(0,m),∴交点到原点的距离相等,∴直线与坐标轴围成的三角形是等腰直角三角形,∴直线PQ与x轴所夹锐角的度数是45°.故答案为x=2;45°.(2)设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,OE>AF,S△POQ=![]() S△PAQ不成立;①当点B落在线段OA上时,如图①,
S△PAQ不成立;①当点B落在线段OA上时,如图①,
![]() ,由△OBE∽△ABF得,
,由△OBE∽△ABF得, ![]() ,∴AB=3OB,∴OB =
,∴AB=3OB,∴OB =![]() OA,由y=x2-4x得点A(4,0),∴OB=1,∴B(1,0),代入y=x+m,∴1+m=0,∴m=-1;②当点B落在线段AO的延长线上时,如图②,
OA,由y=x2-4x得点A(4,0),∴OB=1,∴B(1,0),代入y=x+m,∴1+m=0,∴m=-1;②当点B落在线段AO的延长线上时,如图②,

同理可得OB =![]() OA=2,∴B(-2,0),∴-2+m=0,∴m=2,;综上所述,当m=-1或2时,S△POQ=
OA=2,∴B(-2,0),∴-2+m=0,∴m=2,;综上所述,当m=-1或2时,S△POQ=![]() S△PAQ;
S△PAQ;
(3)①过点C作CH∥x轴交直线PQ于点H,如图③,

可得△CHQ是等腰三角形,∵![]() =45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,∴PH=
=45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,∴PH=![]() PM,∴当PM最大时,PH最大,∴当点P在抛物线顶点处时,PM最大,此时PM=6,∴PH的最大值为6
PM,∴当PM最大时,PH最大,∴当点P在抛物线顶点处时,PM最大,此时PM=6,∴PH的最大值为6![]() ,即PD+DQ的最大值为6
,即PD+DQ的最大值为6![]() .②由①可知:PD+DQ ≤6
.②由①可知:PD+DQ ≤6![]() ,设PD=a,则DQ ≤6
,设PD=a,则DQ ≤6![]() -a,∴PD
-a,∴PD![]() DQ ≤a(6
DQ ≤a(6![]() -a)=-a2+6
-a)=-a2+6![]() a=-(a-3
a=-(a-3![]() )2+18,∵当点P在抛物线的顶点时,a=3
)2+18,∵当点P在抛物线的顶点时,a=3![]() ,∴PD
,∴PD![]() DQ ≤18.;∴PD
DQ ≤18.;∴PD![]() DQ的最大值为18.
DQ的最大值为18.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y=![]() 的图象经过点A.
的图象经过点A.

(1)点E的坐标是 ;
(2)求反比例函数的解析式;
(3)求当一次函数的值小于反比例函数的值时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组进行了如下探究:(1)如图①,若四边形ABCD是矩形,对角线AC、BD交点为P,过点P作PQ⊥BC于点Q,连结DQ交AC于点P1,过点P1作P1Q1⊥BC于点Q1,已知AB=CD=a,则PQ= ,P1Q1= .(用含a的代数式表示)
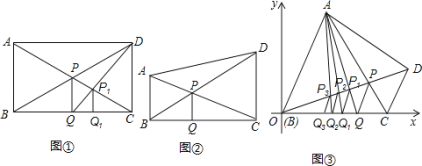
(2)如图②,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AC、BD交于点P,过点P作PQ⊥BC于点Q.已知AB=a,CD=b,请用含a、b的代数式表示线段PQ的长,写出你的解题过程.
(3)如图③,在直角坐标系xOy中,梯形ABCD的腰BC在x轴正半轴上(点B与原点O重合),AB∥CD,∠ABC=60°,AC、BD交于点P,过点P作PQ∥CD交BC于点Q,连结AQ交BD于点P1,过点P1作P1Q1∥CD交BC于点Q1.连结AQ1交BD于点P2,过点P2作P2Q2∥CD交BC于点Q2,…,已知AB=a,CD=b,则点P1的纵坐标为 点Pn的纵坐标为 (直接用含a、b、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.
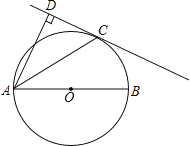
(1)求证:AC平分BAD;
(2)若AC=2![]() ,CD=2,求⊙O的直径.
,CD=2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 各边都相等的多边形是正多边形
B. 正多形的各边都相等
C. 正三角形就是等边三角形
D. 各内角相等的多边形不一定是正多边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com