
【题目】如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.
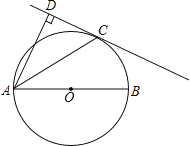
(1)求证:AC平分BAD;
(2)若AC=2![]() ,CD=2,求⊙O的直径.
,CD=2,求⊙O的直径.
【答案】(1)证明见解析;(2)5.
【解析】
试题分析:(1)连接OC,根据切线的性质判断出AD∥OC,得到∠DAC=∠OCA,再根据OA=OC得到∠OAC=∠OCA,可得AC平分∠BAD.
(2)连接BC,得到△ADC∽△ACB,根据相似三角形的性质即可求出AB的长.
试题解析:(1)如图,连接OC,
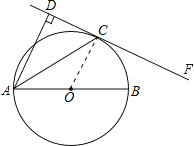
∵DC切⊙O于C,
∴OC⊥CF,
∴∠ADC=∠OCF=90°,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC,即AC平分∠BAD.
(2)连接BC.
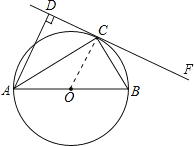
∵AB是直径,
∴∠ACB=90°=∠ADC,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴![]() ,
,
在Rt△ADC中,AC=2![]() ,CD=2,
,CD=2,
∴AD=4,
∴![]() ,
,
∴AB=5.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
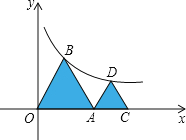
【题目】如图,△OAB和△ACD是等边三角形,O、A、C在x轴上,B、D在y=![]() (x>0)的图象上,则点C的坐标是( )
(x>0)的图象上,则点C的坐标是( )
A.(﹣1+![]() ,0) B.(1+
,0) B.(1+![]() ,0) C.(2
,0) C.(2![]() ,0) D.(2+
,0) D.(2+![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.

(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ;
(2)若两个三角形面积满足S△POQ=![]() S△PAQ,求m的值;
S△PAQ,求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD![]() DQ的最大值.
DQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州市中小学全面开展“体艺2+1”活动,某校根据学校实际,决定开设A:篮球,B:乒乓球,C:声乐,D:健美操等四中活动项目,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图.请回答下列问题:
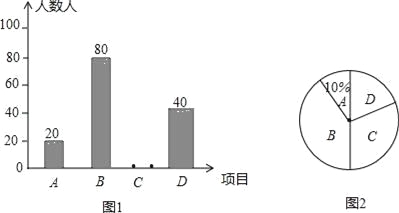
(1)这次被调查的学生共有 人.
(2)请你将统计图1补充完整.
(3)统计图2中D项目对应的扇形的圆心角是 度.
(4)已知该校学生2400人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出一个同时满足下列条件的一元一次方程:①某个未知数的系数是2;②方程的解为3,则这样的方程可写为:_______________________ ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若某一个顶点与和它不相邻的其他各顶点连接,可将多边形分成7个三角形,则这个多边形是( )
A. 六边形 B. 七边形 C. 八边形 D. 九边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
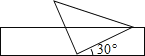
A.3cm B.6cm C.![]() cm D.
cm D.![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com