
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
【答案】(1)A种产品8件,B种产品2件;(2)6种方案(3)当![]() 时可获得最大利润,最大利润为26万元.
时可获得最大利润,最大利润为26万元.
【解析】
试题分析:(1)设生产A种产品x件,则生产B种产品有(10﹣x)件,根据计划获利14万元,即两种产品共获利14万元,即可列方程求解;
(2)根据计划投入资金不多于44万元,且获利多于14万元,这两个不等关系即可列出不等式组,求得x的范围,再根据x是非负整数,确定x的值,x的值的个数就是方案的个数;
(3)得出利润y与A产品数量x的函数关系式,根据增减性可得,B产品生产越多,获利越大,因而B取最大值时,获利最大,据此即可求解.
解:(1)设生产A种产品x件,则生产B种产品(10﹣x)件,于是有
x+3(10﹣x)=14,
解得:x=8,
则10﹣x=10﹣8=2(件)
所以应生产A种产品8件,B种产品2件;
(2)设应生产A种产品x件,则生产B种产品有(10﹣x)件,由题意有:
![]() ,
,
解得:2≤x<8;
所以可以采用的方案有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6种方案;
,共6种方案;
(3)设总利润为y万元,生产A种产品x件,则生产B种产品(10﹣x)件,
则利润y=x+3(10﹣x)=﹣2x+30,
则y随x的增大而减小,即可得,A产品生产越少,获利越大,
所以当![]() 时可获得最大利润,其最大利润为2×1+8×3=26万元.
时可获得最大利润,其最大利润为2×1+8×3=26万元.


科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形是因式分解的是( )
A.6a3b=3a22ab
B.(x+2)(x﹣2)=x2﹣4
C.2x2+4x﹣3=2x(x+2)﹣3
D.ax﹣ay=a(x﹣y)
查看答案和解析>>
科目:初中数学 来源: 题型:
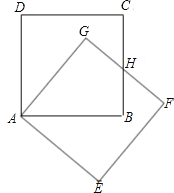
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com