
����Ŀ����ͼ��ʾ����ֱ֪��AB��CD���ڵ�O��![]() ��
��![]() �Ƿ���
�Ƿ���![]() �Ľ⣬Ҳ�Ƿ���
�Ľ⣬Ҳ�Ƿ���![]() �Ľ⣬��
�Ľ⣬��![]() ��
��![]() ��
��
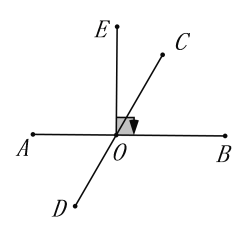
��1����![]() �Ķ�����
�Ķ�����
��2��������OM��OC�������Ƶ�O��![]() ���ٶ�˳ʱ��ת��������ON��OD�������Ƶ�O��
���ٶ�˳ʱ��ת��������ON��OD�������Ƶ�O��![]() ���ٶ���ʱ���һ��ת��������OEֹͣ����ONֹͣʱ��OMҲ��ֹ֮ͣ����ת�������У����˶�ʱ��Ϊt����tΪ��ֵʱ��
���ٶ���ʱ���һ��ת��������OEֹͣ����ONֹͣʱ��OMҲ��ֹ֮ͣ����ת�������У����˶�ʱ��Ϊt����tΪ��ֵʱ��![]() ��
��
��3���ڣ�2���������£���ON�˶���![]() �ڲ�ʱ�����н��ۣ���
�ڲ�ʱ�����н��ۣ���![]() ���䣻��
���䣻��![]() ���䣬����ֻ��һ������ȷ�ģ���ѡ��֤����
���䣬����ֻ��һ������ȷ�ģ���ѡ��֤����
���𰸡���1��30�㣻��2��30��90����3��������ȷ�ģ�֤�����������
��������
��1����![]() ��
��![]() ����
����![]() ��
��![]() �ó�����a��b�ķ����飬�ó�a��b��ֵ���ٸ����ڲ��Ǻʹ�ֱ�Ķ��弴�����
�ó�����a��b�ķ����飬�ó�a��b��ֵ���ٸ����ڲ��Ǻʹ�ֱ�Ķ��弴�����![]() �Ķ���
�Ķ���
��2����t���![]() ��������
��������![]() ��
��![]() ���ⷽ�̼��ɣ�
���ⷽ�̼��ɣ�
��3���ֱ��ʾ��![]() ��
��![]() ���Ӷ��ó�����
���Ӷ��ó�����
��1����![]() ��
��![]() ����
����![]() ��
��![]()
��![]() ����ã�
����ã�![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ����
����![]()
��![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��2����t���![]() ��
��
����ͼ��ʾ��

��![]() ����
����![]()
��![]() ��
��
��![]()
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
����ͼ��ʾ��
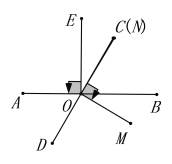
��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��������������ֵΪ30s��90sʱ��![]() ��
��
��3��������ȷ�ģ���ͼ��ʾ�����˶�ʱ��Ϊts��
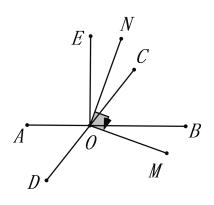
��![]() ��
��![]() ��
��
��![]()
��![]() ��
��
��![]() �Ƕ�ֵ��
�Ƕ�ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
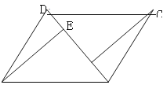
����Ŀ����![]() �У�BD������һ���Խ��ߣ���A��C����ֱ���
�У�BD������һ���Խ��ߣ���A��C����ֱ���![]() ��
��![]() ��E��FΪ���㣮
��E��FΪ���㣮
��1����ͼ����֤��![]() ��
��
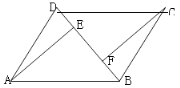
��2����ͼ������AC����AC��BD���ڵ�O����![]() ���ڲ������κθ����ߵ�����£���ֱ��д��ͼ�е����г�����OE����2�����߶Σ�
���ڲ������κθ����ߵ�����£���ֱ��д��ͼ�е����г�����OE����2�����߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵxOy�е�λ����ͼ��ʾ��
��1������ABC���ڵ�C�����ĶԳƵ���A1B1C1��
��2������A1B1C1����ƽ��3����λ������ƽ�ƺ����A2B2C2��
��3����x��������һ��P��ʹPA1+PC2��ֵ��С��������Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+3��a��0��������A����1��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE���AOC����ʱ�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
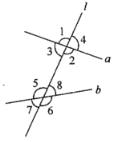
����Ŀ����ͼ��ʾ��ֱ��a��b��ֱ��l���أ���ͼ�жԶ�����______�ԣ��ֱ���_____________���ڲ�����______�ԣ��ֱ���____________��ͬλ����________�ԣ��ֱ���____________���ڴ�����________�ԣ��ֱ���____________��ͬ���ڽ���______�ԣ��ֱ���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�ԭ�㿪ʼ���������ƶ�2cm����A�㣬�������ƶ�4cm����B�㣬Ȼ�������ƶ�10cm����C�㣮
![]()
��1����1����λ���ȱ�ʾ1cm�����������������������ϱ�ʾ��A��B��C�����λ�ã�
��2���ѵ�C����A�ľ����ΪCA����CA��______cm��
��3������B��ÿ��3cm���ٶ������ƶ���ͬʱA��C����ÿ��lcm��5cm���ٶ������ƶ������ƶ�ʱ��Ϊt��t��0���룬��̽��CA��AB��ֵ�Ƿ������t�ı仯���ı䣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() ��ƽ���ı��Σ���
��ƽ���ı��Σ���![]() ��
��![]() �����˶�����
�����˶�����![]() �����
�����![]() ��
��![]() �غϣ�
�غϣ�
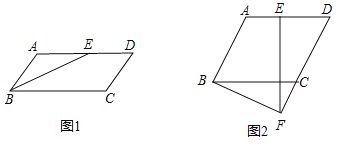
��1����ͼ1������![]() �˶���
�˶���![]() �ߵ��е�ʱ������
�ߵ��е�ʱ������![]() ����
����![]() ƽ��
ƽ��![]() ��֤����
��֤����![]() ��
��
��2����ͼ2������![]() ��
��![]() �ҽ�
�ҽ�![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() ����
����![]() ��
��![]() ��
��![]() �����߶�
�����߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ���ı���
��ʹ���ı���![]() �����Σ������ڣ���˵������
�����Σ������ڣ���˵������![]() ����
����![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() ��ʲôλ��ʱ�ı���
��ʲôλ��ʱ�ı���![]() �����Σ���֤�����������ڣ���˵�����ɣ�
�����Σ���֤�����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�DE�ǡ�ADC��ƽ���ߣ���BC�ڵ�E��
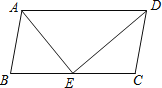
��1����˵��CD=CE��
��2����BE=CE����B=80�㣬���DAE�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com