
【题目】如图所示,直线a,b被直线l所截,则图中对顶角有______对,分别是_____________;邻补角有______对,分别是____________;同位角有________对,分别是____________;内错角有________对,分别是____________;同旁内角有______对,分别是__________.
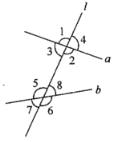
【答案】4 ∠1与∠2,∠3与∠4,∠5与∠6,∠7与∠8 8 ∠1与∠3,∠3与∠2,∠2与∠4,∠1与∠4,∠5与∠8,∠8与∠6,∠6与∠7,∠7与∠5 4 ∠1与∠5,∠3与∠7,∠4与∠8,∠6与∠2 2 ∠3与∠8,∠5与∠2 2 ∠3与∠5,∠8与∠2
【解析】
根据同位角,内错角,同旁内角,对顶角、邻补角的定义解答.
解:直线l截直线a,b所得的对顶角有4对,分别是∠1与∠2,∠3与∠4,∠5与∠6,∠7与∠8;
邻补角有有8对,∠1与∠3,∠3与∠2,∠2与∠4,∠1与∠4,∠5与∠8,∠8与∠6,∠6与∠7,∠7与∠5;
同位角有4对,分别是∠1与∠5,∠3与∠7,∠4与∠8,∠6与∠2;
内错角有2对,它们是∠3与∠8,∠5与∠2;
同旁内角有2对,它们是∠3与∠5,∠8与∠2


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() 经过点A(-5.-6)且与直线
经过点A(-5.-6)且与直线![]() : y=-
: y=-![]() x+6平行,直线
x+6平行,直线![]() 与x轴、y轴分别交于点B,C
与x轴、y轴分别交于点B,C
(1)求直线![]() 的表达式及其与x轴的交点D的坐标:
的表达式及其与x轴的交点D的坐标:
(2)判断四边形ABCD是什么四边形?并证明你的结论:
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标. 请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知直线AB、CD交于点O,![]() ,
,![]() 是方程
是方程![]() 的解,也是方程
的解,也是方程![]() 的解,且
的解,且![]() ,
,![]() .
.
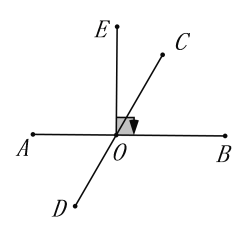
(1)求![]() 的度数.
的度数.
(2)若射线OM从OC出发,绕点O以![]() 的速度顺时针转动,射线ON从OD出发,绕点O以
的速度顺时针转动,射线ON从OD出发,绕点O以![]() 的速度逆时针第一次转动到射线OE停止,当ON停止时,OM也随之停止.在转动过程中,设运动时间为t,当t为何值时,
的速度逆时针第一次转动到射线OE停止,当ON停止时,OM也随之停止.在转动过程中,设运动时间为t,当t为何值时,![]() ?
?
(3)在(2)的条件下,当ON运动到![]() 内部时,下列结论:①
内部时,下列结论:①![]() 不变;②
不变;②![]() 不变,其中只有一个是正确的,请选择并证明.
不变,其中只有一个是正确的,请选择并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学2018年田径运动会上,参加跳高的运动员的成绩如表三所示.
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
(1)写出这些运动员跳高成绩的众数;
(2)该按2017年田径运动会上跳高的平均成绩为1.63m,则该校2018年田径运动会上跳高的平均成绩与2017年相比,是否有提高?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参数同学的成绩,整理并制作如下统计图:

请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)补全频数分布直方图;
(3)在扇形统计图中,m= ,分数段60≤x<70的圆心角= °;
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在 分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、 D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
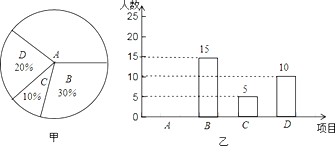
(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com