
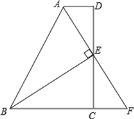
【题目】如图,在△ABF中,BE⊥AF垂足为E,AD∥BC,且AF平分∠DAB,求证:(1)FC=AD;(2)AB=BC+AD.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据平行线性质得到∠DAF=∠F,根据角平分线定义得到∠BAF=∠DAF,进而得到∠F=∠BAF,根据等角对等边得到AB=BF,根据等腰三角形三线合一得到AE=EF,利用ASA证得ADE≌△FCE,即可得证;
(2)由(1)中三角形全等可知AB=BF,AD=FC,利用等量代换即可解决问题.
(1)证明:∵AD∥BC
∴∠DAF=∠F
∵AF平分∠DAB
∴∠BAF=∠DAF
∴∠F=∠BAF
∴AB=BF
又 ∵BE⊥AF
∴AE=EF
在△ADE和△FCE中
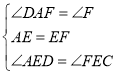
∴△ADE≌△FCE(ASA)
∴FC=AD
(2)证明:∵AB=BF AD=FC
又∵BF=BC+CF
∴AB=BC+AD


科目:初中数学 来源: 题型:
【题目】著名的恩施大峡谷(A)和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路X同侧,AB=50km,A、B到直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图1是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和S1=PA+PB,图2是方案二的示意图(点A关于直线X的对称点是A',连接BA′交直线X于点P),P到A、B的距离之和S2=PA+PB

(1)S1=_____km.S2=_____km.
(2)PA+PB的最小值为_____km.
(3)拟建的恩施到张家界高速公路与沪渝高速公路垂直,建立如图3所示的直角坐标系,B到直线的距为30km,请你在X旁和P旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小,(用尺画出点P和点Q的位置)这个最小值为_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正确的有 .
其中正确的有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,

(1)若∠ABC=30°,∠ACB=50°,求∠DAE的度数
(2)写出∠DAE与∠C-∠B的数量关系,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i为1∶![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )

A. 15米 B. 20![]() 米 C. 20
米 C. 20![]() 米 D. 10
米 D. 10![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=AC=12 厘米,∠B=∠C,BC=8 厘米,点 D 为 AB 的中点.如果点 P 在线段 BC 上以 2 厘米/秒 的速度由 B 点向 C 点运动,同时,点 Q 在线段 CA 上由 C 点向 A 点运动.若点 Q 的运动速度为 v 厘米/秒,则当△BPD 与△CQP 全等时,v 的值为( )

A.2B.5C.1 或 5D.2 或 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,A(-3a,0),B(0,4a),△ABO的面积是6.

(1)求B的坐标.
(2)在x轴的正半轴上有一点C,使∠BAO=2∠BCA,AB=5,动点P从A出发,沿线段AC运动,速度为每秒1个单位长度,设点P的运动时间为t,△BCP的面积为S,用含t的式子来表示S .
(3)在(2)的条件下,在P出发的同时,Q从B出发。沿着平行于x轴的直线,以每秒2个单位长度的速度匀速向右运动,在y轴上是否存在一点R,使△PQR为以PQ为腰的等腰直角三角形,求出满足条件的t,并直接写出点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com