
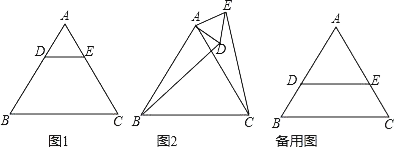
【题目】问题发现:如图1,△ABC是等边三角形,点D是边AD上的一点,过点D作DE∥BC交AC于E,则线段BD与CE有何数量关系?
拓展探究:如图2,将△ADE绕点A逆时针旋转角α(0°<α<360°),上面的结论是否仍然成立?如果成立,请就图中给出的情况加以证明.
问题解决:如果△ABC的边长等于2![]() ,AD=2,直接写出当△ADE旋转到DE与AC所在的直线垂直时BD的长.
,AD=2,直接写出当△ADE旋转到DE与AC所在的直线垂直时BD的长.
【答案】问题发现:BD=CE;拓展探究:结论仍然成立,见解析;问题解决:BD的长为2和2![]() .
.
【解析】
问题发现:如图1,由平行线分线段成比例定理可得BD=CE;
拓展探究:如图2,证明△BAD≌△CAE,可得BD=CE;
问题解决:分两种情况:①如图3,在直角三角形中,根据30°角所对的直角边等于斜边的一半求出DG=1,由勾股定理求出AG=![]() ,得出BG,从而计算出BD的长.
,得出BG,从而计算出BD的长.
②如图4,求EF的长和CF的长,根据勾股定理在Rt△EFC中求EC的长,所以BD=EC=2![]() .
.
解: 问题发现:如图1,BD=CE,理由是
∵△ABC是等边三角形,
∴AB=AC,
∵DE∥BC,
∴BD=CE,
拓展探究:结论仍然成立,如图2,
由图1得,△ADE是等边三角形,
∴AD=AE,
由旋转得∠BAD=∠CAE,△BAD≌△CAE,(旋转的性质)
∴BD=CE,
问题解决:当△ADE旋转到DE与AC所在的直线垂直时,设垂足为点F,此时有两种情况:
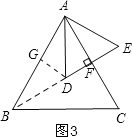
①如图3,
∵△ADE是等边三角形,AF⊥DE,
∴∠DAF=∠EAF=30°,
∴∠BAD=30°,
过D作DG⊥AB,垂足为G,
∵AD=2,
∴DG=1,AG=![]() ,
,
∵AB=2![]() ,
,
∴BG=AB-AG=![]() ,
,
∴BD=2(勾股定理),
②如图4,
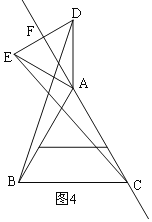
同理得△BAD≌△CAE,
∴BD=CE,
∵△ADE是等边三角形,
∴∠ADE=60°,
∵AD=AE,DE⊥AC,
∴∠DAF=∠EAF=30°,
∴EF=FD=![]() AD=1,
AD=1,
∴AF=![]() ,
,
∴CF=AC+CF=2![]() +
+![]() =3
=3![]() ,
,
在Rt△EFC中,EC=![]() ,
,
∴BD=EC=2![]() .
.
综上所述,BD的长为2和2![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】(初步认识)
(1)如图,将△ABO绕点O顺时针旋转90°得到△MNO,连接AM、BM,
求证△AOM∽△BON.

(拓展延伸)
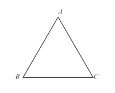
(2)如图,在等边△ABC中,点E在△ABC内部,且满足AE2=BE2+CE2,用直尺和圆规作出所有的点E(保留作图的痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大众服装店今年4月用4000元购进了一款衬衣若干件,上市后很快售完,服装店于5月初又购进该款衬衣,进货量比第一批增加了20%,由于第二批衬衣进货时价格比第一批衬衣进货时价格提高了20元,结果第二批衬衣进货用了6000元
(1)第一批衬衣进货时价格是多少?
(2)第一批衬衣售价为120元/件,为保证第二批衬衣的利润率不低于第一批衬衣的利润率,那么第二批衬衣每件售价至少是多少元?(提示:利润=售价﹣成本,利润率=利润÷成本×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
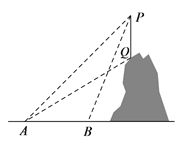
【题目】如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
查看答案和解析>>
科目:初中数学 来源: 题型:
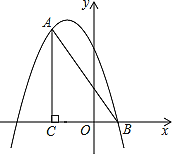
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
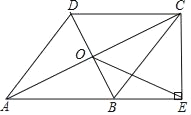
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师让同学们对给定的正方形ABCD,如图.建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,-1),C(1,-1),D(1,0);
丙同学:A(1,0),B(1,-2),C(3,-2),D(3,0);
丁同学:A(-1,2),B(-1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是( )

A. 甲、乙、丙B. 乙、丙、丁C. 甲、丙D. 甲、乙、丙、丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com