
分析 可以设两位数的个位数为x,十位为y,根据两数之和为6,且xy为整数,分别讨论两未知数的取值即可.注意不要漏解.
解答 解:设两位数的个位数为x,十位为y,根据题意得:
x+y=6,
∵xy都是整数,
∴当x=0时,y=6,两位数为60;
当x=1时,y=5,两位数为51;
当x=2时,y=4,两位数为42;
当x=3时,y=3,两位数为33;
当x=4时,y=2,两位数为24;
当x=5时,y=1,两位数为15;
则这样的两位数共有6个,分别是:60、51、42、33、24、15.
故答案为:6;60、51、42、33、24、15.
点评 本题考查了二元一次方程的应用,解题的关键在于根据未知数的整数性质讨论未知数的具体值,注意不要漏掉两位数的个位数可以为0的情况.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
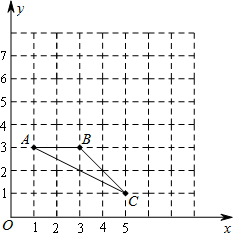 已知△ABC在平面直角坐标系中的位置如图所示.画出△ABC绕点A逆时针旋转90°后的△AB′C′,并写出点B,C的对应点B′,C′的坐标.
已知△ABC在平面直角坐标系中的位置如图所示.画出△ABC绕点A逆时针旋转90°后的△AB′C′,并写出点B,C的对应点B′,C′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=$\sqrt{{x}^{2}-1}$,g(x)=$\sqrt{x+1}$$\sqrt{x-1}$ | ||
| C. | f(x)=($\sqrt{x-1}$)2,g(x)=$\sqrt{(x-1)^{2}}$ | D. | f(x)=$\sqrt{\frac{{x}^{2}-1}{x+2}}$,g(x)=$\frac{\sqrt{{x}^{2}-1}}{\sqrt{x+2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=-7,n=-4 | B. | m=-4,n=-4 | C. | m=-4,n=-1 | D. | m=-5,n=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
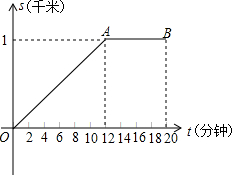 小明早晨从家里出发匀速步行去学校,路上一共用时20分钟.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.设小明从家到学校的过程中,出发t分钟时,他和妈妈所在的位置与家的距离分别为s1(千米)和s2(千米),其中s1(千米)与t(分钟)之间的函数关系的图象为图中的折线段OA-AB.
小明早晨从家里出发匀速步行去学校,路上一共用时20分钟.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.设小明从家到学校的过程中,出发t分钟时,他和妈妈所在的位置与家的距离分别为s1(千米)和s2(千米),其中s1(千米)与t(分钟)之间的函数关系的图象为图中的折线段OA-AB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com