
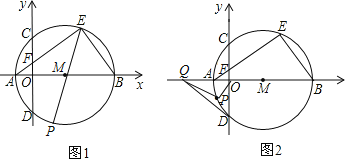
����Ŀ����ͼ1����ƽ��ֱ������ϵ�ڣ�A��BΪx�������㣬��ABΪֱ���ġ�M��y����C��D���㣬CΪ![]() ���е㣬��AE��y���ڵ�F���ҵ�A������Ϊ��2��0����CD��8
���е㣬��AE��y���ڵ�F���ҵ�A������Ϊ��2��0����CD��8
��1�����M�İ뾶��
��2������P�ڡ�M��Բ�����˶���
����ͼ1����FP�ij������ʱ����P��ΪP����ͼ1�л�����P0���������P0������a��ֵ��
����ͼ1����EPƽ�֡�AEBʱ����EP�ij��ȣ�
����ͼ2������D����M�����߽�x���ڵ�Q������P���A��B���غ�ʱ����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
���𰸡���1��r��5����2���ٵ�P0������a��ֵ����3+2![]() ����EP��7
����EP��7![]() ����
����![]() ��
��
��������
��1���ɴ���������֪OD��4������OD��Rt��OMD���ù��ɶ����������r��
��2��������FM���ӳ�����M�ڵ�P��FP�����������֪�ɵ�AF��CF���ɹ��ɶ�����OF��![]() ����P����PH��OB����OFM�ס�HPM�������������ζ�Ӧ�߳ɱ�������MH���������P������꣮
����P����PH��OB����OFM�ס�HPM�������������ζ�Ӧ�߳ɱ�������MH���������P������꣮
�ڹ�P����PG��AE������AP��BP����EPƽ�֡�AEBʱ���ɵ���BAP����EGP��Ϊ����ֱ�������Σ��ɹ��ɶ�������PG��GE��7�������ɵ�EP�ij���
����DQ���M��D�㣬�ɵ���QMD�ס�MDO����MD��MP���ɵ�![]() ������֤����QMP�ס�PMQ������������������������⣮
������֤����QMP�ס�PMQ������������������������⣮
��1����ͼ��1��������OD��

��ֱ��AB��CD��CD��8��
��OD��![]() CD��4��
CD��4��
����MD��MD��MA��r��
��Rt��OMD����OM2+OD2��MD2��
�ã�r��2��2+42��r2�����r��5��
��2������ͼ1��1��������FM���ӳ�����M�ڵ�P����P0��FP�������
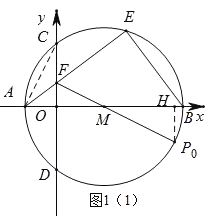
��ֱ��AB��CD��CΪ![]() ���е㣬
���е㣬
��![]() ��
��
���ACF����CAF��
��AF��CF��
��Rt��AFO��OA��2��AF��CF��4��OF��
��OF2+22����4��OF��2����ã�OF��![]() ��
��
��MF��![]() ��
��
��P����PH��OB��
���OFM�ס�HPM��
��![]() ��
��
�� ��
��
��MH��![]() ��
��
���P0������a��ֵ����3+![]() ��
��
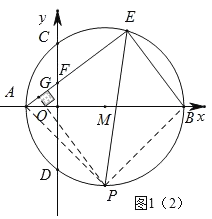
����ͼ1��2��
��![]() ��
��
��![]() ��
��
��AE��CD��8��
��AB��ֱ�������AEB��90����
��P����PG��AE������AP��BP��
��EPƽ�֡�AEBʱ����BAP����BEP����AEP����ABP��45����
��BAP����EGP��Ϊ����ֱ�������Σ���AB��10��
��AP��![]() ��
��
��EG��PG��b����Rt��AGP��PG2+AG2��AP2��
����![]() ,
,
��ã�b��7��b��1����ȥ����
��EP��![]() EG��
EG��![]() ��
��
����ͼ2������PM��DM��
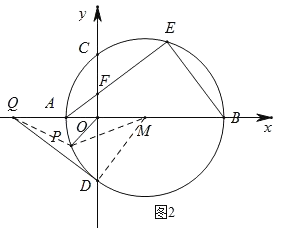
��DQ���M��D�㣬
���MDQ��90������DOM��
���QMD����DMO��
���QMD�ס�MDO��
��![]() ��
��
�֡�MD��MP��
��![]() ��
��
�֡ߡ�OMP����PMQ��
���QMP�ס�PMQ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㴫ͳ�Ļ���У����У�ѧУ�ƻ�ÿ�ܶ���������ڿ�ʱ�俪չ�������չ���ĿΪ����ֽ���������鷨�����֣�Ҫ�����꼶ѧ�����˲μӣ�����ÿ��ֻ�ܲμ�����һ���������ڸ�У���꼶ѧ���������ȡ��100��ѧ�����е��飬���Դ˽���ͳ�ƣ���������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������������
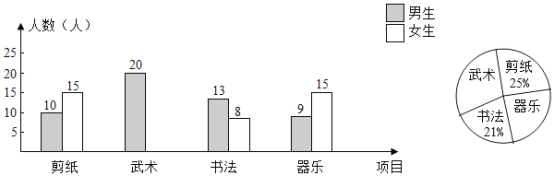
�����������⣺
��1���벹ȫ����ͳ��ͼ������ͳ��ͼ��
��2���ڲμ�����ֽ�����Ŀ��ѧ���У�������ռ�İٷֱ��Ƕ��٣�
��3������У���꼶ѧ������500�ˣ���������вμ����鷨����Ŀ����ж����ˣ�
��4��ѧУ����Ҫ����Щ�������Ů���У������ȡһ���˽�����������ô���ó鵽�μ������������Ŀ��Ů���ĸ����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
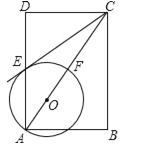
����Ŀ����ͼ���ھ���ABCD�У���O�ڶԽ���AC�ϣ���OA�ij�Ϊ�뾶��ԲO��AD��AC�ֱ��ڵ�E��F������ACB=��DCE��
��1���ж�ֱ��CE����O��λ�ù�ϵ����֤����Ľ��ۣ�
��2����tan��ACB=![]() ��BC=2������O�İ뾶��
��BC=2������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
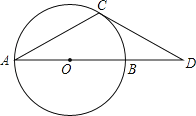
����Ŀ����ͼ��AB����O��ֱ������D��AB���ӳ����ϣ���C����O�ϣ�CA��CD����CDA��30�㣮
��1�����ж�ֱ��CD����O��λ�ù�ϵ����˵�����ɣ�
��2������O�İ뾶Ϊ4��
���ó߹�������A��CD����ֱ�ߵľ��룻
������þ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
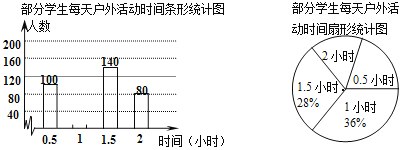
����Ŀ��Ϊ�˽�ѧ���μӻ����������ij�н����������ŶԲ���ѧ���μӻ�����ʱ������˳������飬�������������Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
��1����γ������������� ��ѧ��������ȫ����ͳ��ͼ��
��2����������ͳ��ͼ�б�ʾ����ʱ��0.5Сʱ������Բ�ĽǶ�����
��3��������ε���ѧ���μӻ�����ƽ��ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
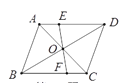
����Ŀ����ͼ��ƽ���ı���ABCD���ܳ���18 cm����Խ���AC��BD�ཻ�ڵ�O������O��ֱ�߷ֱ���AD��BC�ཻ�ڵ�E��F����OE=2 cm�����ı���CDEF���ܳ���_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ�֣���ͼ1�����ı���ABCD�У�AB��DC��E��BC���е㣬��AE����BAD��ƽ���ߣ���AB��AD��DC֮���������ϵΪ_______��
��2������̽������ͼ2�����ı���ABCD�У�AB��DC��E��BC���е㣬��F��DC���ӳ�����һ�㣬��AE����BAF��ƽ���ߣ���̽��AB��AF��CF֮���������ϵ����֤����Ľ��ۣ�
��3������������ͼ3��AB��CD����E���߶�BC�ϣ���BE:EC=3:4����F���߶�AE�ϣ�����EFD =��EAB��ֱ��д��AB��DF��CD֮���������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
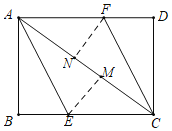
����Ŀ����ͼ��ACΪ����ABCD�ĶԽ��ߣ�����AB��AE�۵���ʹ��B����AC�ϵĵ�M��������CD��CF�۵���ʹ��D����AC�ϵĵ�N����
��1����֤���ı���AECF��ƽ���ı��Σ�
��2������BAEΪ���ٶ�ʱ���ı���AECF�����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ������������ˮƽ����ߣ����Ƕ���ˮƷ�ʵ�����Խ��Խ��.Т���л���˾�����г��������![]() ��
��![]() �����ͺŵľ�ˮ����ÿ̨
�����ͺŵľ�ˮ����ÿ̨![]() �;�ˮ����ÿ̨
�;�ˮ����ÿ̨![]() �;�ˮ�����۶�200Ԫ����5��Ԫ����
�;�ˮ�����۶�200Ԫ����5��Ԫ����![]() �;�ˮ������4.5��Ԫ����
�;�ˮ������4.5��Ԫ����![]() �;�ˮ�����������.
�;�ˮ�����������.
��1����ÿ̨![]() �͡�
�͡�![]() �;�ˮ���Ľ��۸��Ƕ���Ԫ��
�;�ˮ���Ľ��۸��Ƕ���Ԫ��
��2������˾�ƻ�����![]() ��
��![]() �����ͺŵľ�ˮ����50̨��������������
�����ͺŵľ�ˮ����50̨��������������![]() �;�ˮ��Ϊ
�;�ˮ��Ϊ![]() ̨�������ʽ���9.8��Ԫ.����ʱ
̨�������ʽ���9.8��Ԫ.����ʱ![]() �;�ˮ��ÿ̨�ۼ�2500Ԫ��
�;�ˮ��ÿ̨�ۼ�2500Ԫ��![]() �;�ˮ��ÿ̨�ۼ�2180Ԫ.����˾����������
�;�ˮ��ÿ̨�ۼ�2180Ԫ.����˾����������![]() �;�ˮ���������а�ÿ̨����
�;�ˮ���������а�ÿ̨����![]() Ԫ��Ϊ��˾���ƶ������ˮ�����ʽ��軱��˾����50̨��ˮ��������ƶ�ʽ���õ�����Ϊ
Ԫ��Ϊ��˾���ƶ������ˮ�����ʽ��軱��˾����50̨��ˮ��������ƶ�ʽ���õ�����Ϊ![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com