
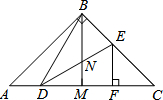
 如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:
如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)设∠EDC=x,则∠DEF=90°-x从而可得到∠DBE=∠DEB=180°-(90°-x)-45°=45°+x,∠DBM=∠DBE-∠MBE=45°+x-45°=x,从而可得到∠DBM=∠CDE;
(2)可证明△BDM≌△DEF,然后可证明:△DNB的面积=四边形NMFE的面积,所以△DNB的面积+△BNE的面积=四边形NMFE的面积++△BNE的面积;
(3)可证明△DBC∽△NEB;
(4)由△BDM≌△DEF,可知DF=BM,由直角三角形斜边上的中线的性质可知BM=$\frac{1}{2}$AC.
解答 解:(1)设∠EDC=x,则∠DEF=90°-x
∴∠DBE=∠DEB=∠EDC+∠C=x+45°,
∵BD=DE,
∴∠DBM=∠DBE-∠MBE=45°+x-45°=x.
∴∠DBM=∠CDE,故(1)正确;
(2)在Rt△BDM和Rt△DEF中,
$\left\{\begin{array}{l}{∠DBM=∠CDE}\\{∠DMB=∠DFE}\\{BD=DE}\end{array}\right.$,
∴Rt△BDM≌Rt△DEF.
∴S△BDM=S△DEF.
∴S△BDM-S△DMN=S△DEF-S△DMN,即S△DBN=S四边形MNEF.
∴S△DBN+S△BNE=S四边形MNEF+S△BNE,
∴S△BDE=S四边形BMFE,故(2)错误;
(3)∵∠BNE=∠DBM+∠BDN,∠BDM=∠BDE+∠EDF,∠EDF=∠DBM,
∴∠BNE=∠BDM.
又∵∠C=∠NBE=45°
∴△DBC∽△NEB.
∴$\frac{CD}{BD}=\frac{BN}{EN}$,
∴CD•EN=BN•BD;故(3)正确;
(4)∵Rt△BDM≌Rt△DEF,
∴BM=DF,
∵∠B=90°,M是AC的中点,
∴BM=$\frac{1}{2}AC$.
∴DF=$\frac{1}{2}AC$,故(4)正确.
故选:C.
点评 本题主要考查的是全等三角形、相似三角形性质和判定,等腰直角三角形的性质,利用面积法证明S△BDE=S四边形BMFE是解答本题的关键.


科目:初中数学 来源: 题型:选择题
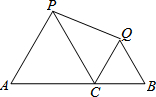 如图,AB=10,C是线段AB上一点,分别以AC、CB为边在AB的同侧作等边△ACP和等边△CBQ,连结PQ,则PQ的最小值是( )
如图,AB=10,C是线段AB上一点,分别以AC、CB为边在AB的同侧作等边△ACP和等边△CBQ,连结PQ,则PQ的最小值是( )| A. | 5 | B. | 6 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
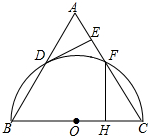 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
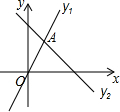 如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )
如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )| A. | x<3时,y1-y2>3 | B. | 当y1>y2时,x>1 | ||
| C. | y1>0且y2>0时,0<x<3 | D. | x<0时,y1<0且y2>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com