
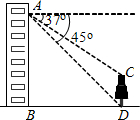
 如图,小林在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为37°,树底D处的俯角为45°,测试点A的高度AB为20米.请你帮助小林计算树的高度(精确到0.1米).
如图,小林在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为37°,树底D处的俯角为45°,测试点A的高度AB为20米.请你帮助小林计算树的高度(精确到0.1米).分析 过点C作CE垂直点A所在的水平线于点E,则在图中得到两个直角三角形,利用三角函数定义分别计算出ED和EC,求差即可.
解答 解:过点C作CE垂直点A所在的水平线于点E,则CE⊥AE,
在Rt△ADE中,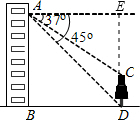
∵∠AED=90°,∠EAD=45°,
∴∠ADE=45°=∠EAD,
∴AE=DE=AB=20,
在Rt△ACE中,
∵∠AED=90°,∠EAC=37°,
∴tan∠EAC=$\frac{CE}{AE}$,
∴CE=AE•tan37°≈20×0.754≈15.1,
∴CD=ED-CE=4.9(米).
答:树的高度约为4.9米.
点评 本题考查了解直角三角形的应用,解答本题的关键是借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
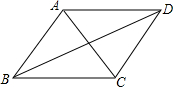 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
如图,下列条件之一能使平行四边形ABCD是菱形的为( )| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com