
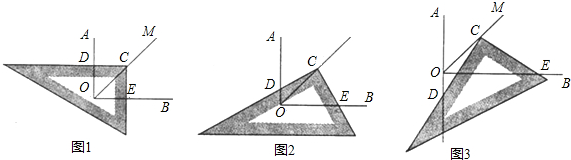
分析 当三角板绕点C旋转到CD与OA垂直时,如图1,只需运用角平分线的性质就可解决问题;当三角板绕点C旋转到CD与OA不垂直时,如图2,图3,过点C作CG⊥OA于G,过点C作CH⊥OB于H,根据角平分线的性质可得CG=CH,易证∠GCH=90°=∠DCE,从而可得∠GCO=∠HCE,进而可得△DGC≌△EHC,即可得到CD=CE.
解答 解:当三角板绕点C旋转到CD与OA垂直时,如图1,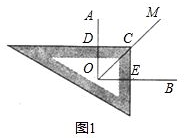
∵OC平分∠AOB,CD⊥OA,CE⊥OB,
∴CD=CE.
当三角板绕点C旋转到CD与OA不垂直时,CD=CE仍然成立.
①如图2,过点C作CG⊥OA于G,过点C作CH⊥OB于H,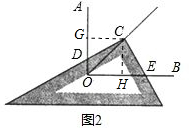
∵OC平分∠AOB,∴CG=CH.
∵∠CGO=∠CHO=∠GOH=90°,
∴∠GCH=90°,
∴∠GCH=∠DCE=90°,
∴∠GCO=∠HCE.
在△DGC和△EHC中,
$\left\{\begin{array}{l}{∠CGD=∠CHE=90°}\\{CG=CH}\\{∠GCD=∠HCE}\end{array}\right.$,
∴△DGC≌△EHC,
∴CD=CE.
②如图3,过点C作CG⊥OA于G,过点C作CH⊥OB于H,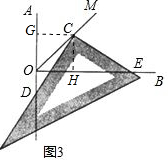
∵OC平分∠AOB,∴CG=CH.
∵∠CGO=∠CHO=∠GOH=90°,
∴∠GCH=90°,
∴∠GCH=∠DCE=90°,
∴∠GCO=∠HCE.
在△DGC和△EHC中,
$\left\{\begin{array}{l}{∠CGD=∠CHE=90°}\\{CG=CH}\\{∠GCD=∠HCE}\end{array}\right.$,
∴△DGC≌△EHC,
∴CD=CE.
点评 本题主要考查了角平分线的性质、全等三角形的判定与性质、四边形的内角和、同角的余角相等等知识,将一般位置与特殊位置相结合是解决本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a、b异号,且|a|>|b| | B. | a、b异号,且|a|<|b| | ||
| C. | a、b异号,且|a|=|b| | D. | a、b异号,且正数的绝对值较大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 82℃ | B. | -82℃ | C. | 412℃ | D. | 247℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
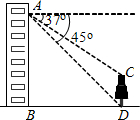 如图,小林在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为37°,树底D处的俯角为45°,测试点A的高度AB为20米.请你帮助小林计算树的高度(精确到0.1米).
如图,小林在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为37°,树底D处的俯角为45°,测试点A的高度AB为20米.请你帮助小林计算树的高度(精确到0.1米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com