
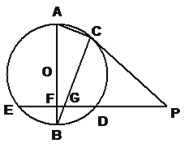
【题目】已知,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
(1)求证:PC是⊙O的切线;
(2)若点C在劣弧AD上运动,其条件不变,问应再具备什么条件可使结论BG2=BF·BO成立,(要求画出示意图并说明理由).
【答案】见解析
【解析】试题分析:(1)证PC是⊙O的切线,即证∠OCP=90°,而∠OCP=∠BCP+∠OCB=∠A+∠OBC,因为AB为直径,直径所对的圆周角为直角,即可证明.
(2)BG2=BFBO要成立,Rt△BFG和Rt△BGO必须相似,而他们已经共用了一角B,所以如果相似,则必有∠BFG=∠BGO=90°,根据垂径定理,G点必在BC中点处.
试题解析:(1)证明:连接OC.∵OA=OC,∴∠A=∠OCA.∵AB为直径,∴∠OCA+∠OCB=90°,∴∠OCP=∠BCP+∠OCB=90°,即PC是⊙O的切线.
(2)解:添加条件为:G为BC的中点.
连接OG.∵G为BC的中点,∴OG⊥BC又FG⊥BO,∴Rt△BFG∽Rt△BGO,∴ ![]() ,即BG2=BFBO.
,即BG2=BFBO.



 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
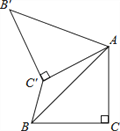
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动
问题情境:
如图1,在ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将ADE绕点A顺时针旋转α角(0°<α<90°)得到AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
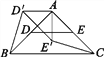 图1
图1 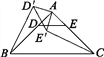 图2
图2 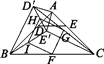 图3
图3 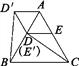 图4
图4
探究发现:
(1)图1中,CE′与BD′的数量关系是________;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E”,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在(2)的条件下,连接BE′,CD′,分别取BC,CD′,E′D′,BE′的中点F,G,H,I,顺次连接F,G,H,I得到四边形FGHI.请判断四边形FGHI的形状,并说明理由;
(4)如图4,在ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将ADE绕点A顺时针旋转60°得到AD′E′,连接CE′,BD′.请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有点![]() 、点
、点![]() .
.
(1)当A、B两点关于x轴对称时,求![]() 的面积;
的面积;
(2)若点A向上平移2个单位,再向右平移3个单位,得到点与点B重合,求A的坐标;
(3)当线段![]() 轴,且
轴,且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王家购买了一套经济适用房,他家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
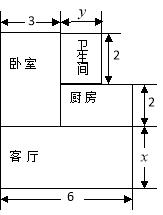
(1)写出用含![]() 、
、![]() 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多21m2,且地面总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
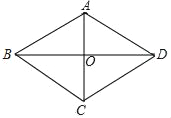
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠BAO=∠DAO.
(1)求证:平行四边形ABCD是菱形;
(2)请添加一个条件使菱形ABCD为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
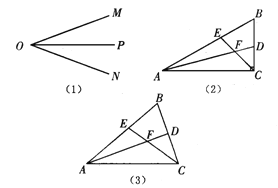
(1)如图(2),在△ABC中,∠ACB是直角,∠B=60°, AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图(3),在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(1)中所得结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,下列说法:①若a+c=0,方程
,下列说法:①若a+c=0,方程![]() 有两个不等的实数根;②若方程
有两个不等的实数根;②若方程![]() 有两个不等的实数根,则方程
有两个不等的实数根,则方程![]() 也一定有两个不等的实数根;③若c是方程
也一定有两个不等的实数根;③若c是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;④若m是方程
成立;④若m是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立.其中正确地只有 ( )
成立.其中正确地只有 ( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com