
【题目】已知等边△ABC,D是BC上一点,E是平面上一点,且DE=AD,∠ADE=60°,连接CE.
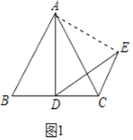
(1)当点D是线段BC的中点时,如图1.判断线段BD与CE的数量关系,并说明理由;
(2)当点D是线段BC上任意一点时,如图2.请找出线段AB,CE,CD三者之间的数量关系,并说明理由;
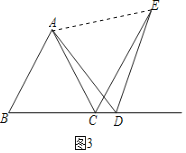
(3)当点D在线段BC的延长线上时,如图3,若△ABC边长为6,设CD=x,则线段CE= (用含x的代数式表示).

【答案】(1)BD=CE,理由见解析;(2)AB=CE+CD,理由见解析;(3)x+6.
【解析】
(1)连接AE,根据等边三角形的判定定理得到△ADE是等边三角形,根据等腰三角形的性质得到AD平分∠BAC,得到AC垂直平分DE,根据线段垂直平分线的定义证明结论;
(2)连接AE,证明△ABD≌△ACE,根据全等三角形的对应边相等解答;
(3)连接AE,证明△ABD≌△ACE,根据全等三角形的对应边相等得到BD=CE,代入计算得到答案.
(1)BD=CE,
证明:如图1,连接AE,
∵DE=AD,∠ADE=60°,
∴△ADE是等边三角形,
∴∠DAE=60°,
∵△ABC是等边三角形,D是BC的中点,
∴AD平分∠BAC,
∴∠DAC=30°,
∵∠DAE=60°,
∴AC平分∠DAE,
∵△ADE是等边三角形,
∴AC垂直平分DE,
∴CE=CD,
∵BD=CD,
∴CE=BD;
(2)AB=CE+CD,
证明:如图2,连接AE,
∵DE=AD,∠ADE=60°,
∴△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
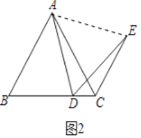
在△ABD和△ACE中,
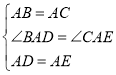
∴△ABD≌△ACE(SAS)
∴BD=CE,
∴AB=BC=BD+CD=CE+CD;
(3)如图3,连接AE,
∵DE=AD,∠ADE=60°,
∴△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
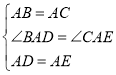 ,
,
∴△ABD≌△ACE(SAS)
∴BD=CE,
∴CE=BD=BC+CD=x+6,
故答案为:x+6.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=6cm,则△DEB的周长为( )
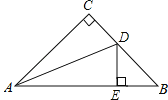
A.4cmB.6cmC.8cmD.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.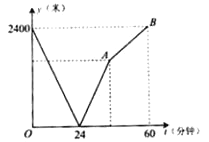
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
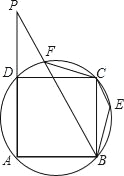
【题目】如图,E,F是正方形ABCD外接圆上的两个点,且EC∥BF,AD与BF的延长线交于点P.
(1)求∠EBF的度数;
(2)求证:BPBE=![]() AB2.
AB2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了解孩子们对《地理中国》 《最强大脑》 《挑战不可能》 《超级演说家》 《中国诗词大会》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:

(1)本次调查共抽取了_________________名学生。
(2)补全条形统计图。
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是__________度。
(4)若该校有1500名学生,请估计喜爱《最强大脑》节目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点C(2,![]() )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
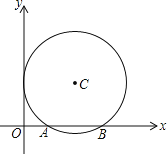
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图,试根据以上提供的信息解答下列问题:
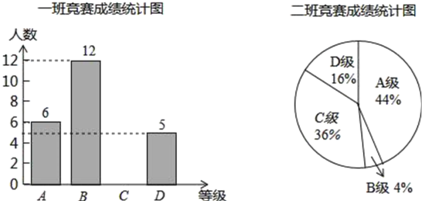
(1)把一班竞赛成绩统计图补充完整;
(2)根据下表填空:a= ,b= ,c= ;
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从平均数和中位数或众数中任选两个对这次竞赛成绩的结果进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凯里市某文具店某种型号的计算器每只进价12元,售价20元,多买优惠,优势方法是:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降价0.1元,例如:某人买18只计算器,于是每只降价0.1×(18﹣10)=0.8(元),因此所买的18只计算器都按每只19.2元的价格购买,但是每只计算器的最低售价为16元.
(1)求一次至少购买多少只计算器,才能以最低价购买?
(2)求写出该文具店一次销售x(x>10)只时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲顾客购买了46只,乙顾客购买了50只,店主发现卖46只赚的钱反而比卖50只赚的钱多,请你说明发生这一现象的原因;当10<x≤50时,为了获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com