【题目】如图，小明同学在点P处测得教学楼A位于北偏东60°方向，办公楼B位于南偏东45°方向．小明沿正东方向前进60米到达C处，此时测得教学楼A恰好位于正北方向．办公楼B正好位于正南方向．求教学楼A与办公楼B之间的距离 ． 
【答案】（60+20 
）米
【解析】解：由题意可知：
∠ACP=∠BCP=90°，∠APC=30°，∠BPC=45°．
在Rt△BPC中，
∵∠BCP=90°，∠B=∠BPC=45°，
∴BC=PC=60．
在Rt△ACP中，
∵∠ACP=90°，∠APC=30°，
tan30°= 
，
∴AC=PCtan30°=tan30°×60=60× 
=20 （米）．
∴AB=AC+BC=60+20 （米）．
答：教学楼A与办公楼B之间的距离是（60+20 ）米．
故答案是：（60+20 ）米．
解直角三角形的基本方法就是把特殊角放在直角三角形中，利用边角关系BC=PC=60，AC=PCtan30°，求出AB.
科目：初中数学 来源： 题型：
【题目】已知：A（0，1），B（2，0），C（4，3）
（1）在直角坐标系中描出各点，画出△ABC．
（2）求△ABC的面积；
（3）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，解答下面的问题：
我们知道方程
有无数个解，但在实际问题中往往只需求出其正整数解．
例：由
，得：
( 
、
为正整数)．要使
为正整数，则
为正整数，可知： 
为3的倍数，从而
，代入
．所以的正整数解为
．
问题：
(1)请你直接写出方程
＝8的正整数解 ．
(2)若
为自然数，则满足条件的正整数
的值有( )
A．3个 B．4个 C．5个 D．6个
(3)关于
， 
的二元一次方程组
的解是正整数，求整数
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，∠ABC＝45°，点D为BC的中点，CE⊥AD于点E，其延长线交AB于点F，连接DF．求证：∠ADC＝∠BDF．
查看答案和解析>>
科目：初中数学 来源： 题型：
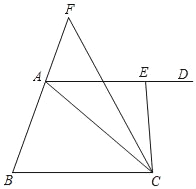
【题目】如图，在△ABC中，∠CAB=∠CBA，过点A向右作AD∥BC，点E是射线AD上的一个动点，∠ACE的平分线交BA的延长线于点F．
（1）若∠ACB=40°，∠ACE=38°，求∠F的度数；
（2）在动点E运动的过程中，
的值是否发生变化？若不变，求它的值；若变化，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与探究
问题情境：如图1，在△ABC中，AB＝AC，点D，E分别是边AB，AC上的点，且AD＝AE，连接DE，易知BD＝CE．将△ADE绕点A顺时针旋转角度α（0°＜α＜360°），连接BD，CE，得到图2．
（1）变式探究：如图2，若0°＜α＜90°，则BD＝CE的结论还成立吗？若成立，请证明；若不成立，请说明理由；
（2）拓展延伸：若图1中的∠BAC＝120°，其余条件不变，请解答下列问题：
从A，B两题中任选一题作答我选择 题
A．①在图1中，若AB＝10，求BC的长；
②如图3，在△ADE绕点A顺时针旋转的过程中，当DE的延长线经过点C时，请直接写出线段AD，BD，CD之间的等量关系；
B．①在图1中，试探究BC与AB的数量关系，并说明理由；
②在△ADE绕点A顺时针旋转的过程中，当点D，E，C三点在同一条直线上时，请借助备用图探究线段AD，BD，CD之间的等量关系，并直接写出结果．
查看答案和解析>>
科目：初中数学 来源： 题型：
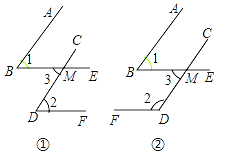
【题目】已知一个角的两边与另一个角的两边分别平行，请结合图，探索这两个角之间的关系，并说明理由．
（1）如图①，AB∥CD，BE∥DF，∠1与∠2的关系是 ；
证明：
（2）如图②，AB∥CD，BE∥DF，∠1与∠2的关系是 ；
证明：
（3）经过上述证明，我们可得出结论，如果一个角的两边与另一个角的两边分别平行，那么这两个角 ；
（4）若这两个角的两边分别平行，且一个角比另一个角的3倍少60°，则这两个角分别是多少度？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
