
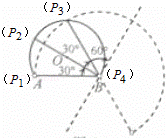
图1和图2中,优弧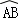 所在⊙O的半径为2,AB=2
所在⊙O的半径为2,AB=2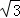 .点P为优弧
.点P为优弧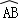 上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
(1)点O到弦AB的距离是 ,当BP经过点O时,∠ABA′= °;
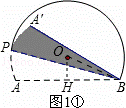
(2)当BA′与⊙O相切时,如图2,求折痕的长:
(3)若线段BA′与优弧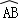 只有一个公共点B,设∠ABP=α.确定α的取值范围.
只有一个公共点B,设∠ABP=α.确定α的取值范围.
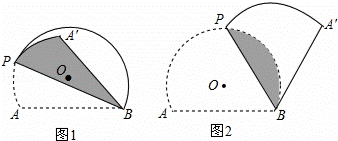
解:(1)①过点O作OH⊥AB,垂足为H,连接OB,如图1①所示.
∵OH⊥AB,AB=2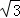 ,
,
∴AH=BH=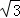 .
.
∵OB=2,
∴OH=1.
∴点O到AB的距离为1.
②当BP经过点O时,如图1②所示.
∵OH=1,OB=2,OH⊥AB,
∴sin∠OBH=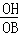 =
=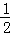 .
.
∴∠OBH=30°.
由折叠可得:∠A′BP=∠ABP=30°.
∴∠ABA′=60°.
故答案为:1、60.
(2)过点O作OG⊥BP,垂足为G,如图2所示.
∵BA′与⊙O相切,
∴OB⊥A′B.
∴∠OBA′=90°.
∵∠OBH=30°,
∴∠ABA′=120°.
∴∠A′BP=∠ABP=60°.
∴∠OBP=30°.
∴OG=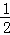 OB=1.
OB=1.
∴BG=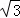 .
.
∵OG⊥BP,
∴BG=PG=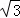 .
.
∴BP=2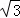 .
.
∴折痕的长为2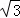 .
.
(3)∵点P,A不重合,∴α>0°,
由(1)得,当α增大到30°时,点A′在 上,
上,
∴当0°<α<30°时,点A′在⊙O内,线段BA′与 只有一个公共点B.
只有一个公共点B.
由(2)知,α增大到60°时,BA′与⊙O相切,即线段BA′与 只有一个公共点B.
只有一个公共点B.
当α继续增大时,点P逐渐靠近B点,但点P,B不重合,
∴∠OBP<90°.
∵α=∠OBA+∠OBP,∠OBA=30°,
∴α<120°.
∴当60°<α<120°时,线段BA′与 只有一个公共点B.
只有一个公共点B.
综上所述:线段BA′与优弧 只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.




 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
下列说法错误的是( )
A. 必然事件的概率为1
B. 数据1、2、2、3的平均数是2
C. 数据5、2、﹣3、0的极差是8
D. 如果某种游戏活动的中奖率为40%,那么参加这种活动10次必有4次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)
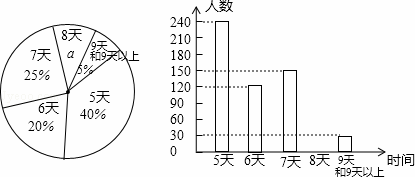
请根据图中提供的信息,回答下列问题:
(1)α= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该地共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com