
【题目】如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0, ![]() ).已知抛物线y=ax2+bx+c经过点A,B,C.
).已知抛物线y=ax2+bx+c经过点A,B,C.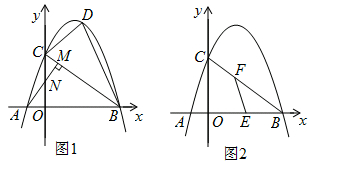
(1)求抛物线的函数式.
(2)连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD= ![]() S△ABC , 求点D的坐标.
S△ABC , 求点D的坐标.
(3)如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.
【答案】
(1)解:∵C(0,3),
∴OC=3,
∵4CN=5ON,
∴ON= ![]() ,
,
∵∠OAN=∠NCM,
∴△AON∽△COB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得OA=1,
,解得OA=1,
∴A(﹣1,0),
设抛物线解析式为y=a(x+1)(x﹣4),
把C(0,3)代入得a1(﹣4)=3,解得a=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣ ![]() x2+
x2+ ![]() x+3
x+3
(2)解:设直线BC的解析式为y=mx+n,
把C(0,3),B(4,0)代入得 ![]() ,解得
,解得 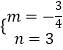 ,
,
∴直线BC的解析式为y=﹣ ![]() x+3,
x+3,
作PQ∥y轴交BC于Q,如图1,设P(x,﹣ ![]() x2+
x2+ ![]() x+3),则Q(x,﹣
x+3),则Q(x,﹣ ![]() x+3),
x+3),
DQ=﹣ ![]() x2+
x2+ ![]() x+3﹣(﹣
x+3﹣(﹣ ![]() x+3)=﹣
x+3)=﹣ ![]() x2+3x,
x2+3x,
∴S△BCD=S△CDQ+S△BDQ= ![]() 4(﹣
4(﹣ ![]() x2+3x)=﹣
x2+3x)=﹣ ![]() x2+6x,
x2+6x,
∵S△BCD= ![]() S△ABC,
S△ABC,
∴﹣ ![]() x2+6x=
x2+6x= ![]() ×
× ![]() ×(4+1)×3,
×(4+1)×3,
整理得x2﹣4x+3=0,解得x1=1,x2=3,
∴D点坐标为(1, ![]() )或(3,3);
)或(3,3);
(3)解:设F(x,﹣ ![]() x+3),则EF=
x+3),则EF= ![]() =
= ![]() ,CF=
,CF= ![]() =
= ![]() x,
x,
点P在整个运动过程中所用时间t= ![]() EF+
EF+ ![]() ,
,
∴ ![]() EF+
EF+ ![]() ≥2
≥2 ![]() ,当EF=
,当EF= ![]() CF时,取等号,此时t最小,
CF时,取等号,此时t最小,
即 ![]() x2﹣
x2﹣ ![]() x+13=(
x+13=( ![]()
![]() x)2得x1=2,x2=
x)2得x1=2,x2= ![]() (舍去),
(舍去),
∴点P在整个运动过程中所用的最少时间2× ![]() ×2=3秒,此时点F的坐标为(2,
×2=3秒,此时点F的坐标为(2, ![]() ).
).
【解析】(1)先证△AON∽△COB,利用相似三角形的性质可求得OA的长,可得A的坐标,从而设抛物线解析式为y=a(x+1)(x﹣4),再把C的坐标代入求出a的值,可得答案;
(2)利用待定系数法求出直线BC的解析式,作PQ∥y轴交BC于Q,设P![]() ,则Q
,则Q![]() ,可表示出DQ,再由S△BCD=S△CDQ+S△BDQ和
,可表示出DQ,再由S△BCD=S△CDQ+S△BDQ和![]() 得到x的方程,解此方程求出x的值,即可得D的坐标;
得到x的方程,解此方程求出x的值,即可得D的坐标;
(3)设E![]() ,表示出EF、CF的长,再由题意得t=
,表示出EF、CF的长,再由题意得t=![]() EF+
EF+![]() ,又
,又![]() ,因为当EF=
,因为当EF=![]() CF时,取等号,此时t最小,进而可得到关于x的方程,解方程求出符合条件的x值,进而可得F的坐标.
CF时,取等号,此时t最小,进而可得到关于x的方程,解方程求出符合条件的x值,进而可得F的坐标.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.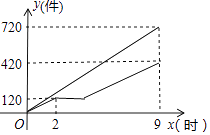
(1)甲车间每小时加工服装件数为件;这批服装的总件数为件.
(2)求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;
(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;……;则第10个图形中,其中看得见的小立方体个数是( )
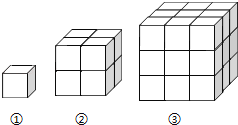
A. 270 B. 271 C. 272 D. 273
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数 ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.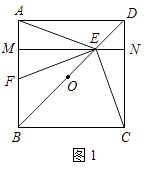
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使 ![]() =
= ![]() =
= ![]() ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;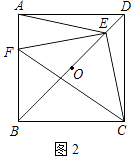
(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 ![]() =
= ![]() 时,请猜想
时,请猜想 ![]() 的值(请直接写出结论).
的值(请直接写出结论).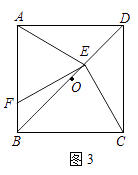
查看答案和解析>>
科目:初中数学 来源: 题型:
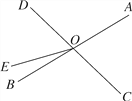
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com