
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.
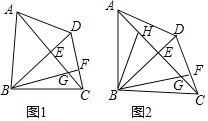
【答案】(1)证明见解析;(2)△ACD、△ABE、△BCE、△BHG.
【解析】(1)由AC⊥BD、BF⊥CD知∠ADE+∠DAE=∠CGF+∠GCF,根据∠BGE=∠ADE=∠CGF得出∠DAE=∠GCF即可得;
(2)设DE=a,先得出AE=2DE=2a、EG=DE=a、AH=HE=a、CE=AE=2a,据此知S△ADC=2a2=2S△ADE,证△ADE≌△BGE得BE=AE=2a,再分别求出S△ABE、S△ACE、S△BHG,从而得出答案.
(1)∵∠BGE=∠ADE,∠BGE=∠CGF,
∴∠ADE=∠CGF,
∵AC⊥BD、BF⊥CD,
∴∠ADE+∠DAE=∠CGF+∠GCF,
∴∠DAE=∠GCF,
∴AD=CD;
(2)设DE=a,
则AE=2DE=2a,EG=DE=a,
∴S△ADE=![]() AE×DE=
AE×DE=![]() ×2a×a=a2,
×2a×a=a2,
∵BH是△ABE的中线,
∴AH=HE=a,
∵AD=CD、AC⊥BD,
∴CE=AE=2a,
则S△ADC=![]() ACDE=
ACDE=![]() (2a+2a)a=2a2=2S△ADE;
(2a+2a)a=2a2=2S△ADE;
在△ADE和△BGE中,
∵ ,
,
∴△ADE≌△BGE(ASA),
∴BE=AE=2a,
∴S△ABE=![]() AEBE=
AEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△ACE=![]() CEBE=
CEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△BHG=![]() HGBE=
HGBE=![]() (a+a)2a=2a2,
(a+a)2a=2a2,
综上,面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在一条直线上,AC=DF,BF=CE,那么添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
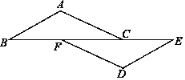
A. ∠A=∠D=90° B. ∠BCA=∠EFD C. ∠B=∠E D. AB=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
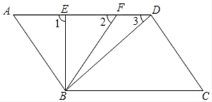
【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合图形填空:已知:如图![]() ,
,![]() .求证:
.求证:![]() .
.
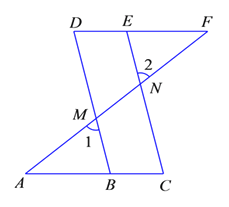
证明:∵![]() (已知),
(已知),
又![]() ( ),
( ),
∴![]() (等量代换),
(等量代换),
∴![]() (同位角相等,两直线平行),
(同位角相等,两直线平行),
∴![]() ( ).
( ).
∵![]() (已知),
(已知),
∴![]() (等量代换),
(等量代换),
∴![]() ( ),
( ),
∴![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )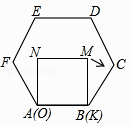
A.1.4
B.1.1
C.0.8
D.0.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com