
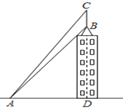
【题目】为了测量大楼顶上(居中)避雷针BC的长度,在地面上点A处测得避雷针底部B和顶部C的仰角分别为55°58′和57°,已知点A与楼底中间部位D的距离约为80米,求避雷针BC的长度.(参考数据:sin55°58′≈0.83,cos55°58′≈0.56,tan55°58′≈1.48,sin57°≈0.84,tan57°≈1.54)
科目:初中数学 来源: 题型:
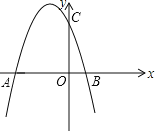
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=![]() OA,直线l2:y=k2x+b经过点C(
OA,直线l2:y=k2x+b经过点C(![]() ,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
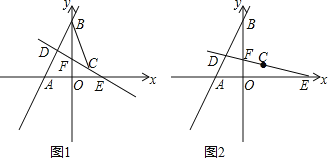
(1)求直线l1的解析式;
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
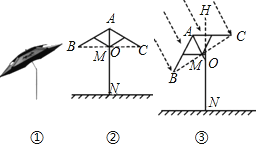
【题目】如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB,AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m,BC与AN交于点M,撑杆AN=2.2m,固定点O到地面的距离ON=1.6m.
(1)如图②,当伞完全撑开并直立时,求点B到地面的距离.
(2)某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.
①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明:![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(![]() ,0)和(m,y),对称轴为直线x=﹣1,下列5个结论:其中正确的结论为_____.(注:只填写正确结论的序号)①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b)
,0)和(m,y),对称轴为直线x=﹣1,下列5个结论:其中正确的结论为_____.(注:只填写正确结论的序号)①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b)
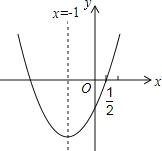
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)中的x与y的部分对应值如表所示,则下列结论中,正确的个数有( )
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
①a<0;②当x<0时,y<3;③当x>1时,y的值随x值的增大而减小;④方程ax2+bx+c=5有两个不相等的实数根.
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com