
分析 (1)根据题意可以分求得y甲(元)、y乙(元)与x(筒)之间的函数关系式;
(2)根据(1)中的函数关系式,利用分类讨论的数学思想可以解答本题;
(3)根据题意可以分别计算出各种方案的花费情况,即可解答本题.
解答 解:(1)由题意可得,
y甲=50×10+(x-10)×10=10x+400,
y乙=(50×10+10x)×0.9=9x+450,
即y甲=10x+400,y乙=9x+450;
(2)当10x+400<9x+450,
解得,x<50,
当10x+400=9x+450,
解得,x=50,
当10x+400>9x+450,
解得,x>50,
由上可得,当购买不足50筒羽毛球时,甲种优惠办法更省钱;当购买50筒羽毛球时,两种优惠办法一样;当购买多于50筒羽毛球时,乙种优惠办法更省钱;
(3)当选择甲种购买方案时,花费为:10x+400=10×60+400=1000,
当选择乙种购买方案时,花费为:9x+450=9×60+450=990,
当选择两种方案时,花费最低为:10×50+(60-10)×10×0.9=950,
由上可得,同时用两种优惠办法购买最省钱.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,利用分类讨论和函数的数学思想解答本题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
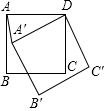 如图,边长为4的正方形ABCD绕点D旋转30°后能与四边形A′B′C′D重合.
如图,边长为4的正方形ABCD绕点D旋转30°后能与四边形A′B′C′D重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com