
分析 (1)规律:两个因数都是两位数,其中十位数字相同,个位数字的和为10,它们的积为:十位数字×(十位数字+1)×100+两个个位数字的积.
(2)将(1)中的数字换成字母按照多项式乘法验证即可.
解答 解:(1)64×66=6×(6+1)×100+4×6=4224,
73×77=7×(7+1)×100+3×7=5621,
81×89=8×(8+1)×100+1×9=7209,
故答案为:4224,5621,7209;
(2)发现的规律为:(10n+a)•(10n+b)=100n(n+1)+ab,
证明:∵a+b=10,
∴等式左边=100n2+10bn+10an+ab=100n2+10n(a+b)+ab=100n2+100n+ab,
右边=100n2+100n+ab,
∴左边=右边,
则(10n+a)•(10n+b)=100n(n+1)+ab.
点评 本题考查了数字的变化规律及整式的运算,解题的关键是观察题意得出规律,并熟练掌握整式的混合运算.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
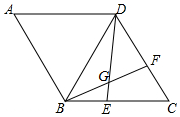 如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为2$\sqrt{7}$.
如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为2$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
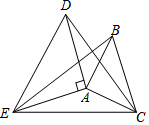 如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )
如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )| A. | ①③ | B. | ②④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
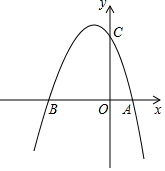 如图所示,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3).
如图所示,抛物线与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com