
【题目】已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.
(1)求证:BD平分∠ABC;
(2)延长AC到点P,使PF=PB,求证:PB是⊙O的切线;
(3)如果AB=10,cos∠ABC=![]() ,求AD.
,求AD.
【答案】
(1)
【解答】证明:∵OD∥BC,
∴∠D=∠CBD,
∵OB=OD,
∴∠D=∠OBD,
∴∠CBD=∠OBD,
∴BD平分∠ABC;
(2)
证明:∵⊙O是以AB为直径的△ABC的外接圆,
∴∠ACB=90°,
∴∠CFB+∠CBF=90°.
∵PF=PB,
∴∠PBF=∠CFB,
由1知∠OBD=∠CBF,
∴∠PBF+∠OBD=90°,
∴∠OBP=90°,
∴PB是⊙O的切线;
(3)
解:连结AD.
∵在Rt△ABC中,∠ACB=90°,AB=10,
∴cos∠ABC=![]() ,
,
∴BC=6,AC=![]() =8.
=8.
∵OD∥BC,
∴△AOE∽△ABC,∠AED=∠OEC=180°﹣∠ACB=90°,
∴![]() ,
,![]() ,
,
∴AE=4,OE=3,
∴DE=OD﹣OE=5﹣3=2,
∴AD=![]() =
=![]() =
=![]() .
.
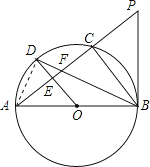
【解析】(1)先由OD∥BC,根据两直线平行内错角相等得出∠D=∠CBD,由OB=OD,根据等边对等角得出∠D=∠OBD,等量代换得到∠CBD=∠OBD,即BD平分∠ABC;
(2)先由圆周角定理得出∠ACB=90°,根据直角三角形两锐角互余得到∠CFB+∠CBF=90°.再由PF=PB,根据等边对等角得出∠PBF=∠CFB,而由(1)知∠OBD=∠CBF,等量代换得到∠PBF+∠OBD=90°,即∠OBP=90°,根据切线的判定定理得出PB是⊙O的切线;
(3)连结AD.在Rt△ABC中,由cos∠ABC=![]() ,求出BC=6,根据勾股定理得到AC=
,求出BC=6,根据勾股定理得到AC=![]() =8.再由OD∥BC,得出△AOE∽△ABC,∠AED=∠OEC=180°﹣∠ACB=90°,根据相似三角形对应边成比例求出AE=4,OE=3,那么DE=OD﹣OE=2,然后在Rt△ADE中根据勾股定理求出AD=
=8.再由OD∥BC,得出△AOE∽△ABC,∠AED=∠OEC=180°﹣∠ACB=90°,根据相似三角形对应边成比例求出AE=4,OE=3,那么DE=OD﹣OE=2,然后在Rt△ADE中根据勾股定理求出AD=![]() =2
=2![]() .
.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题: 
(1)这次被调查的学生共有人.
(2)请将统计图2补充完整.
(3)统计图1中B项目对应的扇形的圆心角是度.
(4)已知该校共有学生3600人,请根据调查结果估计该校喜欢健美操的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据 ![]() =1.732)
=1.732)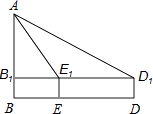
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=![]() GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为![]() 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() ;⑤S四边形CDEF=
;⑤S四边形CDEF=![]() S△ABF , 其中正确的结论有( )
S△ABF , 其中正确的结论有( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com