
����Ŀ��2015��5��6�գ���ɽ�����������������С���Ŀ������̸��������ɳ���������������ͬ����60.8��Ԫ������40ǧ�����������г����ݲ��㣬����24ǧ�ġ����С����������ˮ�ϣ����������½���ϣ�����ÿǧ��ˮ�Ͻ�����ñ�½�ؽ�����ö�0.2��Ԫ��
��1����ÿǧ�ס����С������ˮ�Ͻ�����ú�½�ؽ�����ø��������Ԫ��
��2��Ԥ����ij�Ρ����С�����Ľ����У�ÿ��������Ҫ����ɳʯ1600m3��ʩ���������ô�С�������䳵��10������֪ÿ����ÿ������ɳʯ200m3��ÿ��С��ÿ������ɳʯ120m3����С��ÿ��ÿ������÷ֱ�Ϊ1000Ԫ��700Ԫ����Ҫ��ÿ������ܷ��ò�����9300Ԫ����ʩ�����м�������������������������ͣ���ͷ����Ƕ��٣�
���𰸡���1��1.6��1.4����2�����������������5����5��С��ʱ���������ͣ���ͷ�����8500Ԫ��
��������
�����������1�����ȸ������⣬��ÿǧ�ס����С������ˮ�Ͻ��������Ҫx��Ԫ��ÿǧ��½�ؽ��������y��Ԫ��Ȼ����ݡ����С���Ŀ�ܹ���Ҫ60.8��Ԫ���Լ�ÿǧ��ˮ�Ͻ�����ñ�½�ؽ�����ö�0.2��Ԫ���г���Ԫһ�η����飬�ٽⷽ���飬���ÿǧ�ס����С������ˮ�Ͻ�����ú�½�ؽ�����ø��������Ԫ���ɣ�
��2�����ȸ������⣬��ÿ����m��������Ҫ��10��m��С����Ȼ�����ÿ��������Ҫ����ɳʯ1600m3���Լ�ÿ������ܷ��ò�����9300Ԫ���г�һԪһ�β���ʽ�飬�жϳ�ʩ�����м�������������ֱ����ÿ��������ķ����Ƕ��٣��жϳ����������������ͣ���ͷ����Ƕ��ټ��ɣ�
�����������1����ÿǧ�ס����С������ˮ�Ͻ��������Ҫx��Ԫ��ÿǧ��½�ؽ��������y��Ԫ��
��![]() ����ã�
����ã�![]() ��
��
����ÿǧ�ס����С������ˮ�Ͻ��������Ҫ1.6��Ԫ��ÿǧ��½�ؽ��������1.4��Ԫ��
��ÿǧ�ס����С������ˮ�Ͻ��������Ҫ1.6��Ԫ��ÿǧ��½�ؽ��������1.4��Ԫ��
��2����ÿ����m��������Ҫ��10��m��С����
��![]() ����
����![]() ��
��
��ʩ������3�������������5����5��С��������6����4��С��������7����3��С����
����5����5��С��ʱ�������Ϊ��1000��5+700��5=5000+3500=8500��Ԫ��
����6����4��С��ʱ�������Ϊ��1000��6+700��4=6000+2800=8800��Ԫ��
����7����3��С��ʱ�������Ϊ��1000��7+700��3=7000+2100=9100��Ԫ��
��8500��8800��9100������5����5��С��ʱ���������ͣ���ͷ�����8500Ԫ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
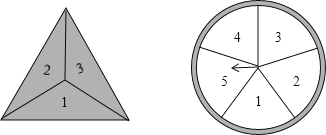
����Ŀ���������ͼ�о��ȵ��������壨��������ĸ������α���1��2��3��4�ĸ����֣�����������ת��ͼ�е�ת�̣�ת�̱��ֳ������ȵ������������
��1�������������ŵص�������ת��ָ����ָ���������֮��Ϊ4�ĸ��ʣ�
��2�������������ŵص�����Ϊa��ת��ָ����ָ�����ڵ�����Ϊb�������x�ķ���![]() ��ʵ�����ĸ��ʣ�
��ʵ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ע�����������ʧ�෴��Ҫ����������֮������˼�ǣ������������������෴����ֱ���������븺�����������5��Ϊ+5�ף���������3��Ϊ��������
A. +5��B. ��5��C. +3��D. ��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��AD �� BC��ֱ��CD���أ�ACΪ��BAD�Ľ�ƽ���ߣ���1+��BCD=180��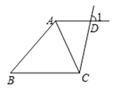
��֤����BCA=��BAC ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����ABC��ƽ���߽�CD�ڵ�E.
��1������A=70�㣬���ABE�Ķ�����
��2����AB��CD���ҡ�1=��2���ж�DF��BE�Ƿ�ƽ�У���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com