
【题目】已知:直线AD , BC被直线CD所截,AC为∠BAD的角平分线,∠1+∠BCD=180°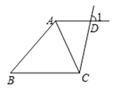
求证:∠BCA=∠BAC .
【答案】证明:方法1 ∵ AD是一条直线,
∴∠1+∠5=180° (平角的定义)或(邻补角的定义)
∵ ∠1+∠BCD=180°(已知)
∴ ∠5=∠BCD(同角的补角相等)
∴ AD∥BC(同位角相等,两直线平行)
∴ ∠4=∠3(两直线平行,内错角相等)
∵ AC为∠BAD的角平分线(已知)
∴ ∠2=∠4(角平分线的定义)
∴ ∠2=∠3(等量代换)
即:∠BCA=∠BAC .
方法2 ∵ AD与CD交于点D ,
∴ ∠1=∠ADC (对顶角相等)
∵ ∠1+∠BCD=180°(已知)
∴ ∠ADC+∠BCD=180°(等量代换)
∴ AD∥BC(同旁内角互补,两直线平行)
∴ ∠4=∠3(两直线平行,内错角相等)
∵AC为∠BAD的角平分线(已知)
∴ ∠2=∠4(角平分线的定义)
∴ ∠2=∠3(等量代换)
即:∠BCA=∠BAC .
【解析】方法1由∠5=∠BCD可证AD∥BC,根据两直线平行,内错角相等得 ∠4=∠3再利用角平分线的定义得∠2=∠4,由等量代换即可求出结果;
方法2由∠ADC+∠BCD=180°可证AD∥BC,根据两直线平行,内错角相等得 ∠4=∠3再利用角平分线的定义得∠2=∠4,由等量代换即可求出结果.
【考点精析】通过灵活运用角的平分线和平行线的判定与性质,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质即可以解答此题.


科目:初中数学 来源: 题型:
【题目】综合题
(1)已知n正整数,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)如图,AB、CD交于点O,∠AOE=90°,若∠AOC︰∠COE=5︰4,求∠AOD的度数.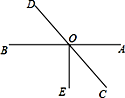
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A:∠B:∠C=l:2:3
B.三边长为a,b,c的值为1,2, ![]()
C.三边长为a,b,c的值为 ![]() ,2,4
,2,4
D.a2=(c+b)(c﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年5月6日,凉山州政府在邛海“空列”项目考察座谈会上与多方达成初步合作意向,决定共同出资60.8亿元,建设40千米的邛海空中列车.据测算,将有24千米的“空列”轨道架设在水上,其余架设在陆地上,并且每千米水上建设费用比陆地建设费用多0.2亿元.
(1)求每千米“空列”轨道的水上建设费用和陆地建设费用各需多少亿元?
(2)预计在某段“空列”轨道的建设中,每天至少需要运送沙石1600m3,施工方准备租用大、小两种运输车共10辆,已知每辆大车每天运送沙石200m3,每辆小车每天运送沙石120m3,大、小车每天每辆租车费用分别为1000元、700元,且要求每天租车的总费用不超过9300元,问施工方有几种租车方案?哪种租车方案费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=(m﹣2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m﹣2)x+2与x轴交于点B. 
(1)求m、n的值;
(2)求△ABO的面积;
(3)观察图象,直接写出当x满足时,y1>y2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com