
【题目】某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.
(1)若公司每天的销售价为x元,则每天的销售量为多少?
(2)如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
科目:初中数学 来源: 题型:
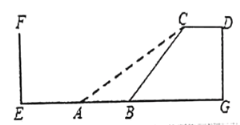
【题目】速滑运动受到许多年轻人的喜爱。如图,四边形![]() 是某速滑场馆建造的滑台,已知
是某速滑场馆建造的滑台,已知![]() ,滑台的高
,滑台的高![]() 为
为![]() 米,且坡面
米,且坡面![]() 的坡度为
的坡度为![]() .后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为
.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为![]() .
.
(1)求新坡面![]() 的坡角及
的坡角及![]() 的长;
的长;
(2)原坡面底部![]() 的正前方
的正前方![]() 米处
米处![]() 是护墙
是护墙![]() ,为保证安全,体育管理部门规定,坡面底部至少距护墙
,为保证安全,体育管理部门规定,坡面底部至少距护墙![]() 米。请问新的设计方案能否通过,试说明理由(参考数据:
米。请问新的设计方案能否通过,试说明理由(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
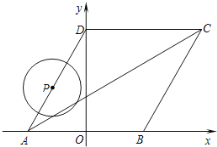
【题目】如图所示,菱形ABCD的顶点A、B在![]() 轴上,点A在点B的左侧,点D在
轴上,点A在点B的左侧,点D在![]() 轴的正半轴上,
轴的正半轴上,![]() ,点A的坐标为
,点A的坐标为![]() .
.
(1)求D点的坐标.
(2)求直线AC的函数关系式.
(3)动点P从点A出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.求
秒.求![]() 为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
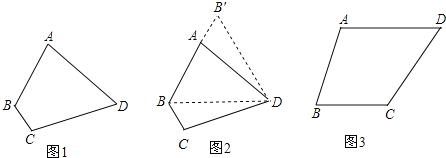
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是 .
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
考点:几何变换综合题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:对于关于![]() 的函数
的函数![]() ,我们称函数
,我们称函数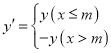 为函数y的m分函数(其中m为常数).
为函数y的m分函数(其中m为常数).
例如:对于关于x一次函数![]() 的
的![]() 分函数为
分函数为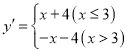
(1)若点![]() 在关于x的一次函数
在关于x的一次函数![]() 的
的![]() 分函数上,求
分函数上,求![]() 的值;
的值;
(2)写出反比例函数![]() 的
的![]() 分函数的图象上y随x的增大而减小的x的取值范围: ;
分函数的图象上y随x的增大而减小的x的取值范围: ;
(3)若![]() 是二次函数
是二次函数![]() 关于x的
关于x的![]() 分函数,
分函数,
①当![]() 时,求y的取值范围;
时,求y的取值范围;
②当![]() 时,
时,![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
③若点![]() ,连结
,连结![]() ,当关于
,当关于![]() 的二次函数
的二次函数![]() 的
的![]() 分函数,与线段MN有两个交点,直接写出m的取值范围.
分函数,与线段MN有两个交点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,EF⊥AC,垂足为点H,分别交AD、AB及CB的延长线交于点E、M、F,且AE:FB=1:2,则AH:AC的值为( )
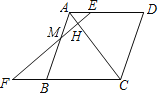
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:① b2-4ac>0;② 2a+b<0;③ 4a-2b+c=0;④ a︰b︰c= -1︰2︰3.其中正确的是【 】
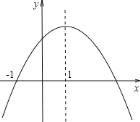
(A) ①② (B) ②③ (C) ③④ (D)①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com