
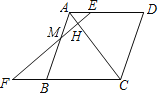
【题目】如图,菱形ABCD中,EF⊥AC,垂足为点H,分别交AD、AB及CB的延长线交于点E、M、F,且AE:FB=1:2,则AH:AC的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接BD,如图,利用菱形的性质得AC⊥BD,AD=BC,AD∥BC,再证明EF∥BD,接着判断四边形BDEF为平行四边形得到DE=BF,设AE=x,FB=DE=2x,BC=3x,所以AE:CF=1:5,然后证明△AEH∽△CFH得到AH:HC=AE:CF=1:5,最后利用比例的性质得到AH:AC的值.
解:连接BD,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,AD=BC,AD∥BC,
∵EF⊥AC,
∴EF∥BD,
而DE∥BF,
∴四边形BDEF为平行四边形,
∴DE=BF,
由AE:FB=1:2,设AE=x,FB=DE=2x,BC=3x,
∴AE:CF=x:5x=1:5,
∵AE∥CF,
∴△AEH∽△CFH,
∴AH:HC=AE:CF=1:5,
∴AH:AC=1:6.
故选:B.



 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】【阅读理解】
某科技公司生产一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分。经核算,2016年该产品各部分成本所占比例约为2:a:1,且2016年该产品的技术成本、制造成本分别为400万元、1400万元。
(1)确定a的值,并求2016年产品总成本为多少万元。
(2)为降低总成本,该公司2017年及2018年增加了技术投入,确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%),制造成本在这两年里都比前一年减少一个相同的百分数2m;同时为了扩大销售量,2018年的销售成本将在2016年的基础上提高10%,经过以上变革,预计2018年该产品总成本达到2016年该产品总成本的![]() 。求m的值。
。求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.
(1)若公司每天的销售价为x元,则每天的销售量为多少?
(2)如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
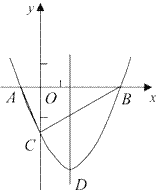
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的动点
中的动点![]() 和图形
和图形![]() ,给出如下定义:如果
,给出如下定义:如果![]() 为图形
为图形![]() 上一个动点,
上一个动点,![]() ,
,![]() 两点间距离的最大值为
两点间距离的最大值为![]() ,
,![]() ,
,![]() 两点间距离的最小值为
两点间距离的最小值为![]() ,我们把
,我们把![]() 的值叫点
的值叫点![]() 和图形
和图形![]() 间的“和距离”,记作
间的“和距离”,记作![]() (
(![]() ,图形
,图形![]() ).
).
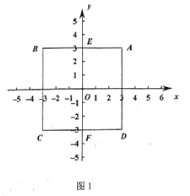
(1)如图,正方形![]() 的中心为点
的中心为点![]() ,
,![]() .
.
①点![]() 到线段
到线段![]() 的“和距离”
的“和距离”![]() (
(![]() ,线段
,线段![]() )=______;
)=______;
②设该正方形与![]() 轴交于点
轴交于点![]() 和
和![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() (
(![]() ,正方形
,正方形![]() )=7,求点
)=7,求点![]() 的坐标.
的坐标.
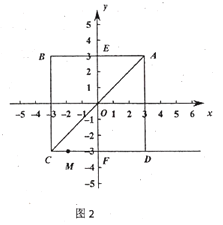
(2)如图2,在(1)的条件下,过![]() ,
,![]() 两点作射线
两点作射线![]() ,连接
,连接![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点,如果
上的一个动点,如果![]() (
(![]() ,线段
,线段![]() )
)![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
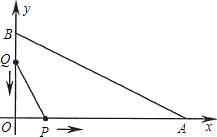
【题目】在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
(1)用含t的代数式表示:线段PO= cm;OQ= cm.
(2)当t为何值时,四边形PABQ的面积为19cm2.
(3)当△POQ与△AOB相似时,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若P和Q两点关于原点对称,则称点P与点Q是一个“和谐点对”,表示为[P,Q],比如[P(1,2),Q(﹣1,﹣2)]是一个“和谐点对”.
(1)写出反比例函数y=![]() 图象上的一个“和谐点对”;
图象上的一个“和谐点对”;
(2)已知二次函数y=x2+mx+n,
①若此函数图象上存在一个和谐点对[A,B],其中点A的坐标为(2,4),求m,n的值;
②在①的条件下,在y轴上取一点M(0,b),当∠AMB为锐角时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
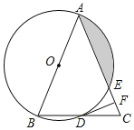
(1)求证:DF为⊙O的切线;
(2)求证:F为CE的中点;
(3)若⊙O的半径为3,∠CDF=22.5°,求阴影部分的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程M为ax2+bx+c=0、N为cx2+bx+a=0(a≠c),则下列结论:①如果5是方程M的一个根,那么![]() 是方程N的一个根;②如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;③如果方程M与方程N有一个相同的根,那么这个根必是x=1.其中正确的结论是( )
是方程N的一个根;②如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;③如果方程M与方程N有一个相同的根,那么这个根必是x=1.其中正确的结论是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com