
【题目】对于平面直角坐标系![]() 中的动点
中的动点![]() 和图形
和图形![]() ,给出如下定义:如果
,给出如下定义:如果![]() 为图形
为图形![]() 上一个动点,
上一个动点,![]() ,
,![]() 两点间距离的最大值为
两点间距离的最大值为![]() ,
,![]() ,
,![]() 两点间距离的最小值为
两点间距离的最小值为![]() ,我们把
,我们把![]() 的值叫点
的值叫点![]() 和图形
和图形![]() 间的“和距离”,记作
间的“和距离”,记作![]() (
(![]() ,图形
,图形![]() ).
).
(1)如图,正方形![]() 的中心为点
的中心为点![]() ,
,![]() .
.
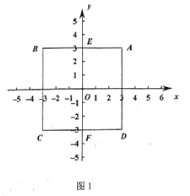
①点![]() 到线段
到线段![]() 的“和距离”
的“和距离”![]() (
(![]() ,线段
,线段![]() )=______;
)=______;
②设该正方形与![]() 轴交于点
轴交于点![]() 和
和![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() (
(![]() ,正方形
,正方形![]() )=7,求点
)=7,求点![]() 的坐标.
的坐标.
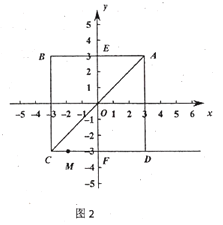
(2)如图2,在(1)的条件下,过![]() ,
,![]() 两点作射线
两点作射线![]() ,连接
,连接![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点,如果
上的一个动点,如果![]() (
(![]() ,线段
,线段![]() )
)![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 取值范围.
取值范围.
【答案】(1)①![]() ;②
;②![]() 的坐标为
的坐标为![]() 和
和![]() ;(2)
;(2)![]() .
.
【解析】
(1)①根据“和距离“的定义计算:OE是两点间距离的最小值,OA是两点间的最大值,相加可得结论;②分两种情况:P在y轴的正半轴和负半轴上,根据“和距离“的定义,并由d(P,正方形ABCD)=7,列方程计算即可;
(2)分M在线段CD上和延长线上两种情况,利用“和距离”的定义列方程可得结论.
(1)①如下图所示,连接OA,
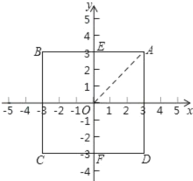
∵四边形ABCD是正方形,且A(3,3),
∴![]() ,
,![]()
∴![]()
即d(O,线段AB)=![]()
故答案为:![]() ;
;
②如下图所示,设![]() ,
,
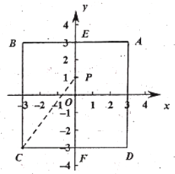
∵点![]() 在线段
在线段![]() 上,
上,
∴![]() .
.
当![]() 时,由题意可知
时,由题意可知![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
∵![]() (
(![]() ,正方形
,正方形![]() )
)![]() ,
,
∴![]() .
.
∴![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
解得![]() .
.
∴![]() .
.
当![]() 时,由对称性可知
时,由对称性可知![]() .
.
综上,![]() 的坐标为
的坐标为![]() 和
和![]() .
.
(2)分两种情况:
①当-3≤t<3时,如下图所示,M在线段CD上,过M作MN⊥AC于N,连接AM,
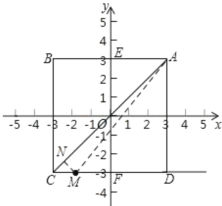
∵M点横坐标是t,
∴CM=t+3,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△CMN是等腰直角三角形,
∴MN=![]() CM=
CM=![]() ,
,
∴![]() (
(![]() ,线段
,线段![]() )=MN+MA=
)=MN+MA=![]() ,
,
②当t≥3时,如下图所示,M在线段CD的延长线上,过M作MN⊥AC于N,
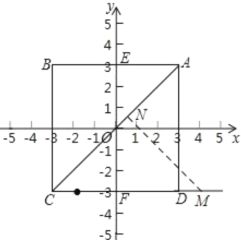
同理可得MN=![]() CM=
CM=![]() ,
,
∴![]() (
(![]() ,线段
,线段![]() )=MN+CM=
)=MN+CM=![]() ,
,
∵M从C到D方向上运动时,MN+MA越来越大,
∴![]()
解得:![]() ,
,
![]()
解得:![]() ,
,
∴![]() 点横坐标
点横坐标![]() 的取值范围是
的取值范围是![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城共有肥料500吨,其中A城肥料比B城肥料少100吨,从A,B城往C,D两乡运肥料的平均费用如表:
A城 | B城 | |
C乡 | 20元/吨 | 15元/吨 |
D乡 | 25元/吨 | 30元/吨 |
现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从B城运往D乡x吨肥料,总运费为y元,求y与x之间的函数关系,并说明如何安排运输才能使得总运费最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
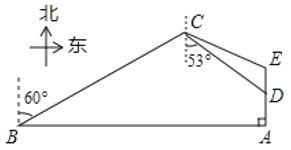
【题目】如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时40海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北2海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.
(1)求CD两点的距离;
(2)渔政船决定再次调整航向前去救援,若两船航速不变,并且在点E处相会合,求∠ECD的正弦值.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别过第二象限内的点![]() 作
作![]() ,
,![]() 轴的平行线,与
轴的平行线,与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与双曲线
,与双曲线![]() 分别交于点
分别交于点![]() ,
,![]() .
.
下面三个结论,
①存在无数个点![]() 使
使![]() ;
;
②存在无数个点![]() 使
使![]() ;
;
③存在无数个点![]() 使
使![]() .
.
所有正确结论的序号是__________.
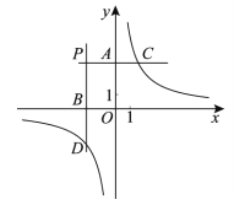
查看答案和解析>>
科目:初中数学 来源: 题型:
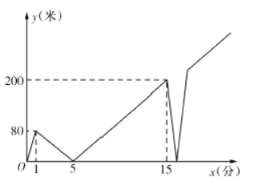
【题目】一天清晨,甲、乙两人在一条笔直的道路上同起点、同终点往返跑步.甲跑了![]() 分钟后乙再出发,当乙追上甲时,甲加快速度往前跑,先到达终点后立刻以加快后的速度返回起点.已知甲加速前、后分别保持匀速跑,乙全程均保持匀速跑下图是甲乙两人之间的距离
分钟后乙再出发,当乙追上甲时,甲加快速度往前跑,先到达终点后立刻以加快后的速度返回起点.已知甲加速前、后分别保持匀速跑,乙全程均保持匀速跑下图是甲乙两人之间的距离![]() (米)与甲跑步的时间
(米)与甲跑步的时间![]() (分)的部分函数图象.则当乙第一次到达终点时,甲距起点______米.
(分)的部分函数图象.则当乙第一次到达终点时,甲距起点______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
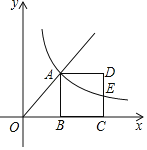
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com