
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是等边三角形.
是等边三角形.
(1)求证:![]() ;
;
(2)求![]() 的度数.
的度数.

【答案】(1)证明见解析(2) 150°.
【解析】
试题分析:(1)根据正方形、等边三角形的性质,可以得到AB=BE=CE=CD,∠ABE=∠DCE=30°,由此即可证明;
(2)只要证明∠EAD=∠ADE=15°,即可解决问题;
试题解析:(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
 ,
,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,
∴∠BAE=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.一个抽奖活动的中奖率是10%,则抽100次奖一定会中奖10次
B.了解某批灯泡的使用寿命,采取普查方式
C.一组数据1、2、3、4的中位数是2.5
D.若甲组数据的方差是S甲2 ,乙组数据的方差是S乙2 ,若S甲2 >S乙2则甲组数据比乙组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC的( )
A. 三边垂直平分线的交点 B. 三条内角平分线的交点
C. 三条高的交点 D. 三条中线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
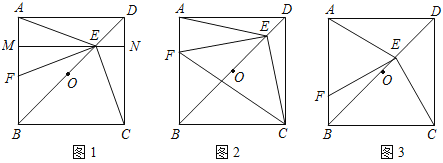
【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使![]() ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;
(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当![]() 时,请猜想
时,请猜想![]() 的值(请直接写出结论).
的值(请直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )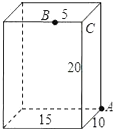
A.5 ![]()
B.25
C.10 ![]() +5
+5
D.35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com