练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】图①、图②、图③均是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1.

    (1)在图①、图②中,以格点为顶点,线段AB为一边,分别画一个平行四边形和菱形,并直接写出它们的面积.(要求两个四边形不全等)

    (2)在图③中，以点A为顶点，另外三个顶点也在格点上，画一个面积最大的正方形，并直接写出它的面积。

    【答案】（1）菱形的面积=4；平行四边形的面积=4；作图见解析（2）正方形的面积=10，作图见解析.

    【解析】

    （1）根据菱形和平行四边形的画法解答即可；

    （2）根据勾股定理逆定理，结合网格结构，作出最长的线段作为正方形的边长即可．

    (1)如图①②所示：

    菱形的面积=4；平行四边形的面积=4；

    (2)如图③所示：

    正方形的面积=10

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是

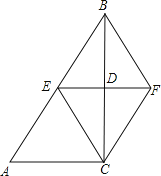
    A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：若线段上的一个点把这条线段分成1：2的两条线段，则称这个点是这条线段的三等分点．如图1，点C在线段AB上，且AC：CB＝1：2，则点C是线段AB的一个三等分点，显然，一条线段的三等分点有两个．

    （1）已知：如图2，DE＝15cm，点P是DE的三等分点，求DP的长．

    （2）已知，线段AB＝15cm，如图3，点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动；点Q从点B出发，先向点A方向运动，当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm，设运动时间为t秒．

    ①若点P点Q同时出发，且当点P与点Q重合时，求t的值．

    ②若点P点Q同时出发，且当点P是线段AQ的三等分点时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年的 “十一”黄金周是天的长假，某风景区在天假期中每天旅游人数变化如表（正号表示人数比前一天多，符号表示比前一天少）

    日期

    日

    日

    日

    日

    日

    日

    日

    日

    人数变化单位：万人

    （1）若月日的游客人数为万人，则月日的旅客人数为_________万人；

    （2）八天中旅客人数最多的一天比最少的一天多_______万人

    （3）如果每万人带来的经济收入约为万元，则黄金周八天的旅游总收入约为多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小聪从家里跑步去体育场，在那里锻炼了一会儿后，又走到文具店去买笔，然后走回家，如图是小聪离家的距离（单位：）与时间（单位：）的图象。根据图象回答下列问题：

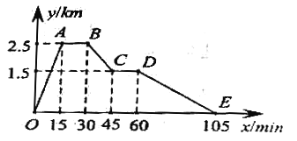
    （1）体育场离小聪家______；

    （2）小聪在体育场锻炼了______；

    （3）小聪从体育场走到文具店的平均速度是______；

    （4）小聪在返回时，何时离家的距离是？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某天早上，一辆交通巡逻车从A地出发，在东西向的马路上巡视，中午到达B地，如果规定向东行驶为正，向西行驶为负，行驶纪录如下:（单位：km）

    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    第七次

    +15

    －8

    +6

    +12

    －4

    +5

    －10

    （1）B地在A地哪个方向，与A地相距多少千米？

    （2）巡逻车在巡逻过程中，离开A地最远是多少千米？

    （3）若每km耗油0.1升，问共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中,规定：抛物线y=a(xh) +k的关联直线为y=a(xh)+k.

    例如：抛物线y=2(x+1) 3的关联直线为y=2(x+1)3，即y=2x1.

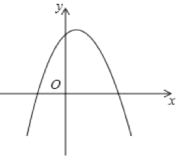
    (1)如图,对于抛物线y=(x1) +3.

    ①该抛物线的顶点坐标为___，关联直线为___，该抛物线与其关联直线的交点坐标为___和___；

    ②点P是抛物线y=(x1) +3上一点,过点P的直线PQ垂直于x轴,交抛物线y=(x1) +3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0)，求当d随m的增大而减小时，d与m之间的函数关系式，并写出自变量m的取值范围。

    (2)顶点在第一象限的抛物线y=a(x1) +4a与其关联直线交于点A,B(点A在点B的左侧)，与x轴负半轴交于点C，直线AB与x轴交于点D，连结AC、BC.

    ①求△BCD的面积(用含a的代数式表示).

    ②当△ABC为钝角三角形时，直接写出a的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2017浙江省湖州市，第23题，10分）湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了20000kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本=放养总费用+收购成本）．

    （1）设每天的放养费用是a万元，收购成本为b万元，求a和b的值；

    （2）设这批淡水鱼放养t天后的质量为m（kg），销售单价为y元/kg．根据以往经验可知：m与t的函数关系为；y与t的函数关系如图所示．

    ①分别求出当0≤t≤50和50＜t≤100时，y与t的函数关系式；

    ②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值．（利润=销售总额﹣总成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

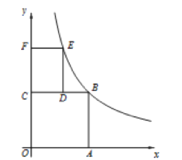
    【题目】如图，正方形OABC的边OA，OC在坐标轴上，矩形CDEF的边CD在CB上，且5CD=3CB，边CF在轴上，且CF=2OC-3，反比例函数y= (k>0)的图象经过点B,E，则点E的坐标是____

    查看答案和解析>>

    同步练习册答案