
【题目】如图,已知四边形ABCD是矩形,点E,G分别是AD,BC边的中点,连接BE,CE,点F,H分别是BE,CE的中点连接FG,HG.
(1)求证:四边形EFGH是菱形;
(2)当![]() = 时,四边形EFGH是正方形.
= 时,四边形EFGH是正方形.
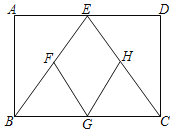
【答案】(1)见解析;(2)![]()
【解析】
(1)先连接EG,根据四边形ABGE、四边形GCDE都是矩形,得出EF=FG,EH=GH,再根据四边形EFGH是平行四边形,得出FG=EH,最后得到EF=FG=GH=EH,即可得出结论;
(2)根据有一个角是直角的菱形是正方形进行判断即可.
解:(1)连接EG,
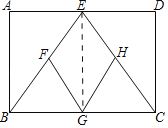
∵矩形ABCD中,AD=BC,E,G分别是AD,BC的中点,
∴AE=BG,
又∵AE∥BG,∠A=90°,
∴四边形ABGE是矩形,
∴∠BGE=90°,
∵F是BE的中点,
∴Rt△BEG中,EF=![]() BE=GF,①
BE=GF,①
同理可得,EH=![]() CE=GH,②
CE=GH,②
∵EG⊥BC,BG=GC,
∴BE=EC,
∴EF=EH,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形;
(2)当AB边和AD边之间满足条件:AD=2AB时,四边形EFGH是正方形.
理由:当AB边和AD边之间满足AD=2AB时,四边形ABGE与四边形EGCD都是正方形,
故∠FGE=∠EGH=45°,
∴∠FGH=90°,
∴菱形EFGH是正方形.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
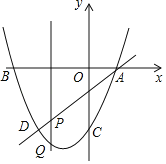
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 均为的等边三角形,点
均为的等边三角形,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 与
与![]() 平行的直线交射线
平行的直线交射线![]() 于点
于点![]() .
.
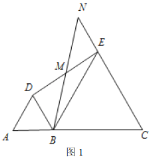
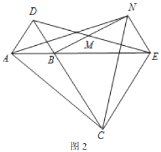
(1)当![]() ,
,![]() ,
,![]() 三点在同一直线上时(如图1),求证:
三点在同一直线上时(如图1),求证:![]() 为
为![]() 中点;
中点;
(2)将图1中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() ,
,![]() ,
,![]() 三点在同一直线上时(如图2),求证:
三点在同一直线上时(如图2),求证:![]() 为等边三角形;
为等边三角形;
(3)将图2中![]() 绕点
绕点![]() 继续顺时针旋转多少度时,点
继续顺时针旋转多少度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点,试作出图形并直接写出
中点,试作出图形并直接写出![]() 绕点
绕点![]() 继续旋转的度数.
继续旋转的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
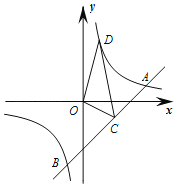
【题目】如图,已知直线y=x﹣3与双曲线y=![]() (k>0)交于A、B两点,点A的纵坐标为1.
(k>0)交于A、B两点,点A的纵坐标为1.
(1)求点B的坐标;
(2)直接写出当x在什么范围内时,代数式x2﹣3x的值小于k的值;
(3)点C(2,m)是直线AB上一点,点D(n,4)是双曲线y=![]() 上一点,将△OCD沿射线BA方向平移,得到△O′C′D′.若点O的对应点O′落在双曲线y=
上一点,将△OCD沿射线BA方向平移,得到△O′C′D′.若点O的对应点O′落在双曲线y=![]() 上,求点D的对应点D′的坐标.
上,求点D的对应点D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
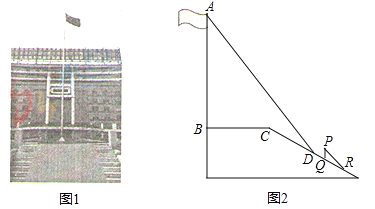
【题目】(2016山东省烟台市)某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.
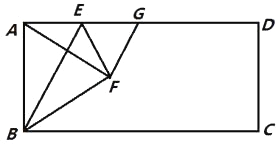
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y = ax2 2ax + c图像的顶点为P,与x轴交于A、B两点(其中点A在点B的左侧),与y轴交于点C,它的对称轴交直线BC交于点D,且CD︰BD=1︰2.
(1)求B点坐标;
(2)当△CDP的面积是1时,求二次函数的表达式;
(3)若直线BP交y轴于点E,求当△CPE是直角三角形时的a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,BC=CD,连接AC、BD,∠ADB=90°.
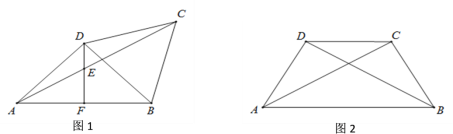
(1)如图1,若AD=BD=BC,过点D作DF⊥AB于点F,交AC于点E:
①∠DAC= °;
②求证:EC=EA+ED;
(2)如图2,若AC=BD,求∠DAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com